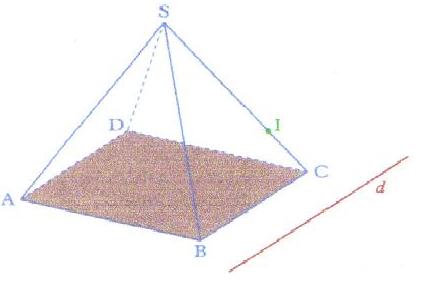
Je pense que on doit tracer une parallèle à d, mais je ne vois pas où.
quelqu'un peut-il m'aider ?

bonsoir,le plan P coupe le plan de base suivant d
le plan SBC coupe le plan de base suivant BC qui est//d
donc l'intersction des plans P et SBC est // d  (et BC) c'est donc la //BC menée par I

merci pour votre réponse.

J'ai encore unn petit souci dans un exercice du même type dont voici le sujet :

Soit ABCDEFGH un cube de côté 4 cm, O le centre du cube et O' le centre de la face ABCD.

1. Montrer que (EC) est orthogonale au plan (BDG)
2. S est le point d'intersection de (EC) et (BDG). Montrer que S appartient à la droite (GO')
3. a. Tracer la section du cube par le plan (AEG) en vraie grandeur.
4. Que représente S pour le triangle DGB ?

Pouvez-vous vérifier si ces réponses sont correctes :

1. Pour cela, il faut que je trouve deux droites sécantes aux plans... enfin il me semble... le seul problême c'est que je ne les trouve pas.

2. Je pense qu'il faut que je dise que : (GO') appartient au plan (BDG)
   Mais après je n'arrive pas à prouver que S appartient à cette droite.

3.a. voir dessin

b. Le point S représente le centre de gravité du triangle, faut-il le prouver ?

merci d'avance

oups petit problême, le dessin du post précédent représente la section demandé en question 3

et voici le cube original :

DB est perpendiculaire à EA et cG donc au plan EACG donc à toute droite de ce plan et en particulier à ECOn va montrer que EC est perpendiculaire à O'G on aura

ainsi EG perpendiculaire à DB et à O'G deux droites du plan BDG
donc EG sera perpendiculaire au plan BDG
les triangles EGC etO'CG sont rectanlgles et O'C/CG=(a2/2)/a
CG/EG=a/(a2)
donc O'C/CG=CG/EG{smb]racine[/smb]2/2
et les deux triangles sont semblables
on en déduit que angle GO'C=angleECG

désolée j'ai des problèmes avec les symboles  et les envois
je réécris  O'C/CG=CG/EG=(2)/2

si K est l'intersection de EC et O'G le triangle GKC est rectangle en HK donc EC est perpendiculaire à O'G

d'accord merci pour votre réponse.