Inscription / Connexion Nouveau Sujet
Solution analytique, vectorielle, etc...
Bonjour à tous.
Je demande une aide concernant un exercice sur les vecteurs.
** image supprimée **
je dois trouver la solution analytique, vectorielle puis géométrique.
Pour le 1a, j'ai déja noté :
(v() pour vecteur)
v(AD) = 1/2 v(AC) soit D(1/2;0)
v(AE) = 1/3 v(AB) soit E(0;1/3)
v(AF) = v(AB) + 2 V(BC) soit F (1;2)
b. ...
2a. v(DE) = - 1/3 v(AB) + 1/2 v(AC)
v(DF) = 1/2 v(AC) + ( 2 v(BC) ??)
b. ...
Pour le 3, et la figure j'ai fait ça :
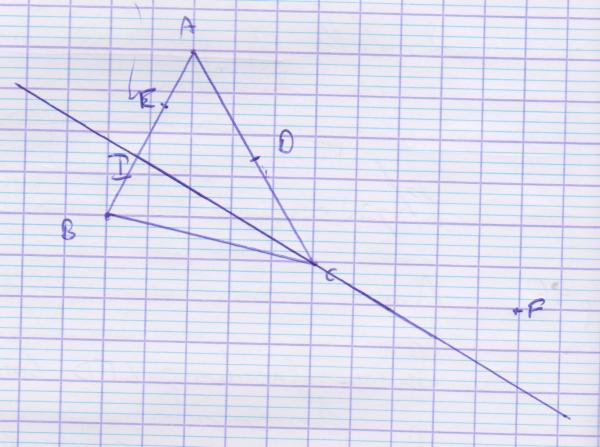
Et pour la démonstration, il me semble qu'il faut utiliser Thalès, enfin je en suis pas vraiment sur...
Aidez-moi svp.
* Océane > lilgreg97one si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
Bonsoir
en vecteurs
ED=EA+AD=-AB/3+AC/2
EF=EB+BF=2/3AB+2BC=2/3AB+2(BA+AC)
=-4/3AB+2AC
et tu vois bien que l'on a
EF=4ED et par conséquent les 2 vecteurs sont colinéaires et donc les 3 points sont alignés.
géométrique:
(ED) est la droite des milieux dans le triangle AIC donc;...
et vue la position de E sur [AB]
tu as AE=EI=IB
et dans le triangle BEF
(IC) est donc la droite des milieux dans le triangle
et donc....
analytique
A(0;0)
B(1;0)
C(0;1)
E(1/3;0)
D(1/2;1/2)
comme C est le milieu de [BF]
xc=(xB+xF)/2 xF=2xC-xB je te laisse calculer
yF=2yc-yB - - - - - - -
tu écris alors les équations de (ED) et de (EF) et tu montres qu'elles ont meême coefficient directeur
Bonjour la Guadeloupe. (que je connais assez bien)
dans ce que j'ai écrit dans mon précédent post, il y a une erreur
en effet
A(0;0)
B(1;0)
C(0;1)
E(1/3;0)
D(0;1/2) (l'erreur était sur le coordonées de ce point)
Pour F tu utilises bien ce que j'ai écrit.
xF=2xC-xB=0-1=-1
yF=2yC-yB=2-0=2
F(-1;2))
quand une droite (PQ) passe par les 2 points P et Q, tu as appris que le coefficient directeur de cette droite est donnée par
a=(yQ-yP)/(xQ-xP)
il faut donc que tu moontres que les coeffcients directeurs des 2 droites (ED) et (EF) sont égaux donc que
(yF-yE)/(xF-xE)=(yD-yE)/(xD-xE)
et tu sauras bien trouver l'égalité (-3/2)


