Bonsoir.   Tu as le cas particulier du tétraèdre trirectangle, dont les trois faces supérieures sont des triangles rectangles isocèles, et donc les trois angles adjacents au sommet sont des angles droits .

    C'est tout simplement le " coin " d'un cube ou d'un pavé ...

Merci pour votre réponse.

Ce que je sais de la pyramide : les trois triangles sont rectangles mais ne sont pas isocèles.

Il n'y a donc pas de propriété ?

Bonne soirée,

    Ce doit etre le même principe ...  le coin d'un cube, mais dissymétrique  

Ok merci, je vais voir ça

Bonjour,

Je reviens avec une autre question au sujet des pyramides, voici le dessin :


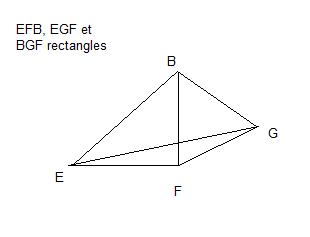
Puis-je dire que l'angle EBG et égal à l'angle EBF + l'angle GBF ?

La perspective m'embête un peu à vrai dire ..

Merci d'avance,

    Non, tu ne peux pas ...
Si c'est une question de dessin, fais donc la vue " d'avion "... Tu verras que ces angles ne peuvent pas être égaux, sauf si le point F était sur le côté EG, donc si le trièdre était aplati !...

Erf :x c'est ce que je redoutais.

Donc comment faire ?
J'avais pensé à passer par le triangle EBG, mais ne sachant pas si il est rectangle ou non, je suis bloqué.

Pour info, le prof nous demande "Calculer EBF et GBF" puis "Peut-on en déduire EBG ?".
J'avais calculé les angles grâce à la trigo.

    Et tu connais quoi dans ces 2 triangles ?..

Alors :
Je connais BF, FG, EF.
Je pourrais connaître facilement : EB, BG et EG.

Je connais les angles EBF et FBG.
Donc je connais aussi les angles BEF et BGF.

(les triangles EFG, EFB et FBG étant rectangles).

Voilà, c'est tout ce que je connais de ma pyramide.

Merci,

   Dans le 1er triangle(devant moi), qui semble rectangle en F, tu connais FE et FB ....  
    Qu'attends tu  pour en déduire les angles qui t'intéressent ?...

Et pour EBG,  peut-être Al-Kashi ...   cherche un peu !

Ah oui, je peux calculer les angles BEG et BGE, merci de me l'avoir fait remarquer

Bonne soirée,

    Je crois que tu te moques de moi ...

Je viens de réaliser que ce n'était pas possible en fait.

Désolé si vous pensez que je me moque de vous, mais je ne vois pas quels autres angles calculer avec mes données autres que BEF et BGF.

Et le théorème d'Al Kashi, jamais vu en classe. Ca m'étonnerais que le prof nous demande de l'utiliser, mais je peux toujours me renseigner si il le faut.

Merci de votre patience en tout cas,

    Que connais-tu dans le triangle  BEF ?...

Je connais ses trois côtés et ses trois angles.
De même pour le triangle BFG.

Je cherche encore mais je ne trouve pas
Je serais bien tenté de répondre "Non", car généralement, quand le prof ne nous demande pas de démontrer mais s'il est possible de le démontrer, la réponse est non.

    Si , dans le triangle  BEG, tu connais la longueur des côtés, tu peux dessiner ce triangle , le représenter en vraie grandeur sur un plan,  donc tu connais ce traingle ...
    Tu n'as peut-être une formule toute faite sous la main, mais tu peux mesurer les angles ...

Connais tu les angles dans BEG ?...

Dans BEG je peux trouver toutes les mesures des côtés (en gros je connais toutes les mesures des arrêtes de la pyramide) mais pour les angles, je ne pense pas (BEG est quelconque).

Ah, donc vous suggérez que je mesure moi-même les angles ?
Car comme le triangle est pas rectangle, je ne peux pas trouver les angles, en tout cas pas avec le programme de troisième.