Inscription / Connexion Nouveau Sujet
Somme suite avec algorithme
Bonsoir,
Je bloque depuis 3 jours sur un exercice, si quelqu'un pouvait m'aider un peu ça serait sympa (:
Données :
f(x) = sqrt(1-x^2)
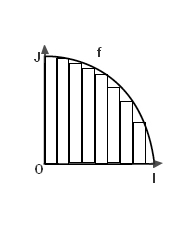
A_n = 1/n [f(1/n) + f(2/n) + f(3/n) + ... + f(n/n)] (somme aires des n rectangles construits en dessous de Cf)
A'_n = 1/n [f(0) + f(1/n) + f(2/n) + .... + f((n-1)/n)] (somme aires de n rectangles au dessus de Cf)
A est l'aire du domaine delimité par [OI), [OJ) , (Cf) et la droite d'équation x=1
A_n<= A <= A'_n et A'_n - A_n = 1/n
1) Déterminer le plus petit entier naturel non nul n tel que A_n soit une valeur approchée de 
/4 à 10^-3 près
2)Ecrire un algorithme calculant une valeur approchée de /4 à 10^-p près en fonction de A_n (avec n un entier dépendant de p qui sera saisi)
Bonjour,
1) explication de l'exercice
la fonction f(x) décrit un quart de cercle de centre O et de rayon 1. cela peut se prouver (grâce à Pythagore).
donc l'aire délimitée par OI, OJ et la courbe de f est un quart de disque de centre O et de rayon OI.
(Je ne vois pas pourquoi le prof a ajouré "délimité par la droite d'équation x=1, car ca n'enlève pas le moindre petit point au domaine, mais passons.)
Son aire vaut donc un quart de l'aire d'un disque de rayon 1.
Aire du disque complet : 
R²=*1*1 =
=> A = / 4
2) valeurs approcée
Il semble que tu aies prouvé (ou que l'énoncé affirme sans le prouver) que A_n<= A <= A'_n et A'_n - A_n = 1/n
a) Pour être exact, on va d'abord prouver que A_n et A'_n sont des valeurs approchées de A à au plus 1/n.
c'est à dire que | A_n - A | <= 1/n
et | A'_n - A | <= 1/n
b) Ensuite, on répond à la question du prof : pour quelle valeur de n obtient-on une valeur approchée à 10^-3 près.
c'est à dire qu'on cherche la première valeur de n telle que (1/n) 
10^-3
Merci déjà pour la réponse, j'y vois déjà un peu plus clair,
sauf que je ne suis pas sûre d'avoir bien compris le raisonnement à la fin : " c'est à dire qu'on cherche la première valeur de n telle que (1/n) 10^-3 " on cherche n tel que A_n vaut environ /4 , c'est à dire A_n A , Mais quand je cherche n tel que (1/n) 10^-3 , je tombe sur un nombre très grand, ce qui semble peu cohérent quand on le remplace dans l'expression de A_n
J'ai peut être mal saisi...
Merci Barney, mais je n'ai pas encore appris les formes du type "∫√(1-x²)dx" , je ne peut pas les utiliser dans un devoir
Bonsoir,
Personnellement, je m'arrêterais à An - A'n <= 1/n
ce qui permet de déduire presuqe immédiatement que |A'n - Pi/4| <= 1/n
et |An - Pi/4| <= 1/n
si je prends n=1000, j'ai don,c la certitude que An et A'n sont des estimations de Pi/4 à 10^-3 près.
Maintenant la version pointilleuse :
Il faudrait prouver que A_n est une suite croissante ou A'_n une suite décroisaante.
Ainsi tu pourras affirmer, par exmple (à vérifier) :
|A_573 - Pi/4| > 10^-3
|A_574 - Pi/4| <= 10^-3
donc n=574 est la première valeur pour laquelle l'approximation est <= 10^-3
Annuler
connectez vous