Inscription / Connexion Nouveau Sujet
Statistique
Bonjour, j'ai un problème pour une question d'un exercice qui me laisse perplexe.
Les tableaux ci dessous donnent le nombre de naissances (en milliers) par an en France métropolitaine entre 1901 et 1920
1) b) Donner la médiane, les premier et troisième quartiles de cette série statistique.
J'ai réussi les autres exercices mais celui ci me perturbe car ce n'est pas un tableau : valeur/effectif
Merci d'avance pour votre aide
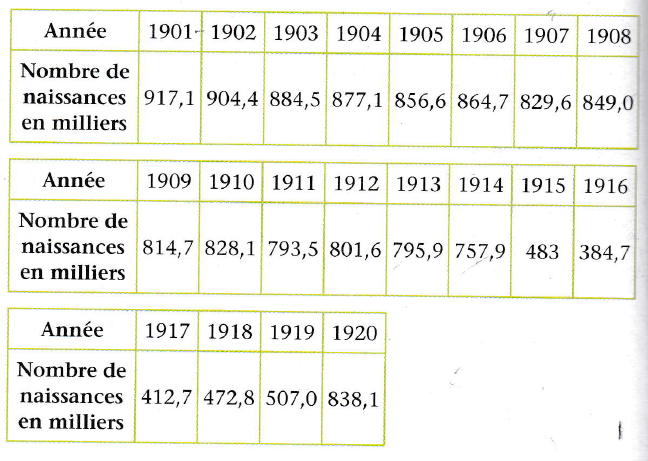
La médiane il me semble l'avoir trouvée. Étant donné qu'il y a 20 valeurs la médiane se situe entre la 9eme et la 10eme valeur, soit Me = (828.1+814.7)/2 = 821.4
Est ce bien cela ?
Mais j'ai du mal à trouver les quartiles
Pour un problème dont l'effectif total serait 120, on calculerait Q1 = (120*25)/100 et Q3= (120*75)/100
et en fonction des valeurs trouvées , on trouverait le 1er et 3ème quartiles
mais sur cet exercice, je bloque :/
Bonsoir
la série doit être ordonnée dans l'ordre croissant (sort A sur les calculatrices)
la médiane est alors une valeur comprise entre la dixième et la onzième valeur
N'aurais tu pas vu en cours la méthode des effectifs cumulés croissants pour serrer miner médiane et quartiles ?
Bonsoir
la série doit être ordonnée dans l'ordre croissant (sort A sur les calculatrices)
la médiane est alors une valeur comprise entre la dixième et la onzième valeur

N'aurais tu pas vu en cours la méthode des effectifs cumulés croissants pour serrer miner médiane et quartiles ?
Si il me semble, on fait cumule les effectifs, on calcule Q1 et Q3 puis on cherche les énièmes valeurs données dans le cumul des effectif ? c'est ça ?
Par exemple si Q1 = 45, on cherche la valeur de la 45 ème donnée ?
Merci pour vos réponses en tout cas

non certainement pas si vous écrivez ceci cela veut dire que Q1=N/4
Q1 est la valeur dont le rang est N/4 s'il y a 180 données N/4 =45 et on cherche à quoi correspond la quarante-cinquième valeur
les 10 premières valeurs ordonnées
médiane moyenne entre 814.7 et 828.1
Q1 cinquième valeur (20/4=5) donc Q1=507
ici l' effectif pour chaque valeur est 1 donc ce n'est pas la peine de calculer les effectifs cumulées croissants
J'avoue que mes réponses sont au sommum de la stupidité.
Je pense que j'ai très mal lu le sujet.
Répondre que l'effectif est le nombre de fois où apparit la valeur observée n'est pas entièrement fausse dans le cas général. Mais ici avec le contexte cela voudrait dire qu'une année apparaîtrait plusieurs milliers de fois. Je n'avais pas lu la première ligne.
Toutes mes plates excuses. 
J'avoue que mes réponses sont au sommum de la stupidité.
Je pense que j'ai très mal lu le sujet.
Répondre que l'effectif est le nombre de fois où apparit la valeur observée n'est pas entièrement fausse dans le cas général. Mais ici avec le contexte cela voudrait dire qu'une année apparaîtrait plusieurs milliers de fois. Je n'avais pas lu la première ligne.
Toutes mes plates excuses.

Pas de soucis, ça arrive à tout le monde, merci beaucoup d'avoir pris le temps de me répondre

non certainement pas si vous écrivez ceci cela veut dire que Q1=N/4
Q1 est la valeur dont le rang est N/4 s'il y a 180 données N/4 =45 et on cherche à quoi correspond la quarante-cinquième valeur
les 10 premières valeurs ordonnées
médiane moyenne entre 814.7 et 828.1
Q1 cinquième valeur (20/4=5) donc Q1=507
ici l' effectif pour chaque valeur est 1 donc ce n'est pas la peine de calculer les effectifs cumulées croissants
Oui, je suis d'accord avec toi, or le corrigé me dit Q1=632 e Q3=860 , sans explications, et vu que je ne trouve pas pareil, je pensais avoir faux c'est pour cela que j'ai posté l'exercice ici, pour voir où est mon erreur dans mes calculs
Bonjour
le corrigé n'a pas pris la même définition des quartiles que celle de l'enseignement en France
En France Q1 est la valeur du caractère dont le rang est le plus petit entier supérieur ou égal à N/4
là ils ont considéré la première partie de la série et ont pris pour Q1 la définition de la médiane à savoir celle qui partage la série en deux parties de même effectif.
la série a 20 valeurs
on coupe en 2 pour former deux séries de 10 valeurs
puis on recoupe chacune de ces séries en 2 et on prend une valeur qui partage la série en deux de même effectif donc on va prendre la moyenne de la cinquième et la sixième valeur
pour Q3 ce sera la moyenne entre la quinzième et seizième valeur
c'est d'ailleurs cette méthode qu'on a choisi pour certaines calculatrices donc se méfier


