Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première StatistiquesTopics traitant de statistiques [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Statistiques

Posté par
DreamBoy 10-11-17 à 17:57

Bonjour,

je suis coincé à cette question-ci :
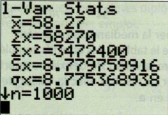
(Il m'est donné un écran de calculatrice cf. image)
Calculer la valeur exacte de la variance de cette série. puis vérifier qu'elle est
égale au carré de l'écart type donné par la calculatrice.

J'ai la formule V(x)=\frac{1}{n}\sum_{i=1}^{k}n$_{i}x$_{i}²-\bar{x}
qui fait V(x)=\frac{1}{n}\sum{x}-\bar{x}²

Du coup je remplace et j'ai \frac{3472400-58.27²}{1000} qui fait environ 3469 mais ça vaut pas du tout le carré de sigma minuscule

Merci d'avance de votre aide

Posté par
DreamBoyre : Statistiques 10-11-17 à 17:58

J'ai oublié d'attacher l'image :S

Statistiques

Posté par
verdurinre : Statistiques 10-11-17 à 18:13

Bonsoir.
Attention
ta formule demande de calculer

\dfrac{3472400}{1000} -58.27^2

Posté par
DreamBoyre : Statistiques 10-11-17 à 18:54

DreamBoy @ 10-11-2017 à 17:57


V(x)=\frac{1}{n}\sum{x}-\bar{x}²


Correction
V(x)=\frac{1}{n}(\sum{x²})-\bar{x}²

Posté par
DreamBoyre : Statistiques 10-11-17 à 18:56

verdurin

Ah ouiii merci ! le résultat est bon maintenant

oui c'est vrai que x barre ne se somme pas

Merci !

Posté par
verdurinre : Statistiques 10-11-17 à 20:21

service


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !