Inscription / Connexion Nouveau Sujet
Suite arithmétique dans un graphique
Bonjour à tous,
je me présente je susi un élève de 1ereS et nous avons étudié très rapidement les suites car nous sommes en retard. Mais voilà le professeur n'a pas tré bien expliqué et le cours n'est pas très explicite.Il nous a donné un exercice un peu complexe pour voir si nous avions compris mais franchement je en vois pas comment procéder pour y arriver . J'espère que vous pourrez m'aidez a terminer cet exercice en vous remerciant d'avance.L'exercice est le suivant:
Soit (Un)la suite définie sur U0=1/2 et pour tout naturel n , Un+1 =Un/(1+2Un) .
1) Conjecturez graphiquement le comportement de la suite (Un) .
2) Prouvez que la suite (Vn) est artihmétique;donnez son premier terme et sa raison ?
3) Exprimez Vn, puis Un, en fonction de n
J'ai vraiment besoin d'aide 
Cordialement.
Bonjour,
Pour la question 1, il faut faire un graphique ressemblant à celui-ci et essayer de conjecturer le comportement de la suite.
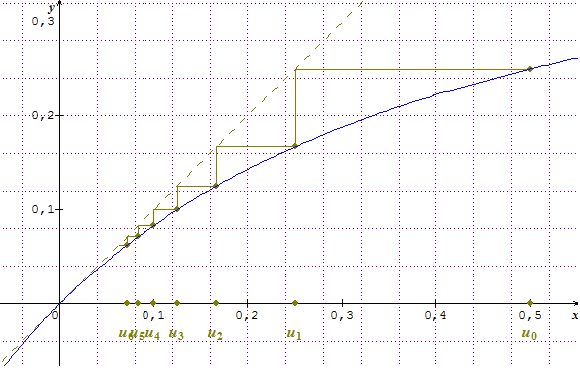
Pour les questions 2 et 3 il manque une information dans l'énoncé : comment est définie la suite v ?
Bonjour,
tout d'abord merci de m'avoir répondu.En effet j'ai oublié de mettre la suite (Vn)qui est définir par
Vn=(1/Un)+1 . Et j'aurais une question si vous me le permetter j'aimerais comprendre comment trouver les coordonnées de la courbe. En ordonnée il me semble qu'il faut calculer U0,U1... mais comment calculer les points en abscisse.Merci.
Cordialement.
La courbe correspond à celle de la fonction f définie par f(x)=x/(1+2x). En effet, on peut remarquer que un+1=f(un).
On part de u0 sur l'axe des abscisses.
On regarde le point de coordonnées (u0,f(u0))=(u0,u1).
On repart vers le point de coordonnées (un+1,un+1) qui se trouve sur la droite en pointillés d'équation y=x)
On regarde ensuite le point de coordonnées (un+1,un+2) sur la courbe ... etc.
Ok merci de m'avoir répondu je vais tracer le graphique et comment je dosi procéder pour les questions 2) et 3) ?
Et si j'ai bien compris en fait les coordonnées des points sont (u0;u1) (u1;u2)... ?
Oui

Pour la question 2, il faut calculer vn+1-vn et démontrer qu'il s'agit d'une constante : c'est assez facile.
La question 3 découle de la question 2. Si on trouve la raison r de la suite arithmétique (v) alors vn=v0+nr
Bonjour,
merci d'avoir était patient avec moi j'ai pu terminer mon terminer mon exercice et meiux comprendre la leçon.
Passez une bonne journée et bonne continuation.
Cordialement.
Bonsoir, je viens de lire cet exercice qui ressemble fort au mien et je ne comprends pas comment vous faites pour la question 3, pourriez-vous m'expliquez.
Merci à vous.
À la question 2, on démontre que la suite (v) est arithmétique et que sa raison est r=1.
On en déduit alors que vn=v0+nr, soit vn= (1/u0)+1+n.
Or u0=0,5 donc v0=3
Donc vn=3+n.
Or vn=(1/un)+1. À partir de là, il suffit d'isoler un et de l'exprimer en fonction de vn puis de n.



