Inscription / Connexion Nouveau Sujet
Suite arithmétique, géométrique
Bonsoir, j'a un ex a faire pendant les vacances le voici : le soir avant de s'endormir Bachir regarder série ou un livre. La probabilité qu'il :
- lis le soir s'il l'a lu la veille est de 0,3
- lise le soir si la regarder des séries la veille est de 0,7
Pour tout entier naturel non nul, on note Ln l'événement "le n-ieme soir, Bachir lit un livre" et on appelle on, la probabilité de cette évènement.
Le premier soir, Bachir a lu un livre de sorte que p=1
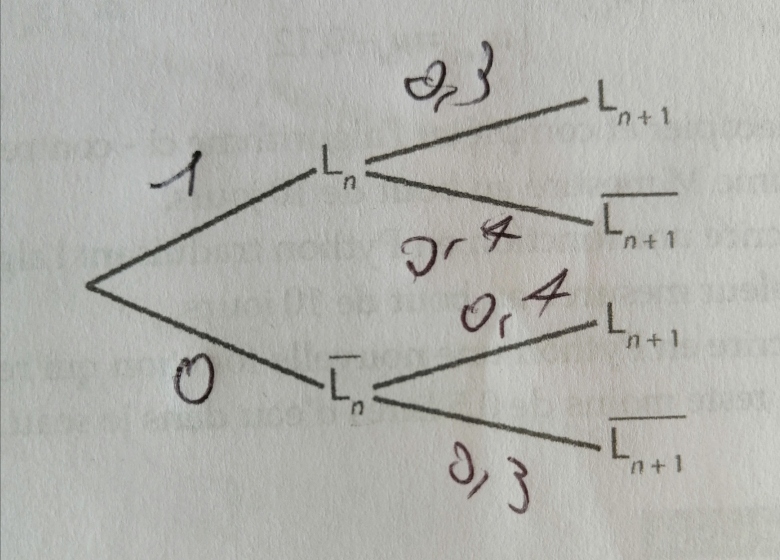
1) recopier et compléter l'arbre ci-contre représentant la situation(image ci-dessous)
2) montrer que Pn+1=-0,4pn+0,
La suite (pn) est-elle arithmétique ou géométrique ?
3)on définit pour tout n appartenant à N la suite (vn) par vn=pn-0,5
Montrer que vn+1=-0,4pn+0,2
Alors je suis totalement perdue pour la 1... En soit faut til montrer que cette suite est arithmétique par rapporte à la relation de pn ? Car cette dernière dépend de Pn donc elle est ni arithmétique ni géométrique ? Mais comment le rédiger ?
La 3 j'avais trouver mais je pense pas que j'ai bon... Car j'ai déterminé l'expression de pn avec celle de pn+1 :
Pn=- 0,4(n-1)+0,7
Pn=-0,4n+0,4+0,7
Donc : vn=-0,4pn+0,4+0,7-0,5
vn=-0,4pn+0,6
On déterminé vn+1 :
Vn+1=-0,4(n+1)+0,6
Vn+1=-0,4n-0,4+0,6
Vn+1=-0,4pn+0,2
Cela me partait bizarre de passer de n à Pn
Merci d'avance

bonsoir
calcule les premiers termes de la suite
pour montrer que la suite n'est pas arithmétique, il suffit que tu donnes un contre exemple...
idem pour montrer que la suite n'est pas géométrique.
montre ton arbre complété, et ce que tu as fait pour 2)
Pn=- 0,4(n-1)+0,7 n'est pas correct
ps : relis l'énoncé que tu as écrit :
Bachir a lu un livre de sorte que p=1 ---- c'est p0=1 ou p1 = 1 ?
et
2) montrer que pn+1=-0,4pn+0, ?
(image ci dessous)
Il faut que je calcul les premiers termes de la suite, en effet mais il faut que je montre pour cela que vn+1=-0,4pn+0,7?
J'ai fais sur ma calculette, et effectivement elle est ni géométrique et arithmétique... Mais il faut que je le démontre ? Et ça je ne sais pas comment ? Ah moin de donner un contre exemple je ne vois pas
Ps: c'est P1=1

bonjour Stracth47
énoncé : et on appelle on, ? la probabilité de cette évènement.
pour que ton arbre soit généraliste, i.e. qu'il soit exploitable quelle que soit la valeur de n,
sur la branche Ln, tu dois écrire pn (et non pas 1)
sur la branche Lnbarre, à la place de 0 , tu dois écrire ...? (quelle probabilité en fonction de pn?)
ainsi corrigé, tu pourras plus facilement répondre à la première partie de la question 2)
2) quelles valeurs trouves-tu pour les premiers termes ?
montre le détail de tes calculs si besoin.
pas arithmétique : comme déjà dit, il suffit de trouver un contre exemple.
par ex : calcule p2 - p1, puis p3 - p2
puis relis la définition d'une suite arithmétique
que peux-tu en conclure ?
je m'absente un peu
si une autre intervenant souhaite prendre le relais...
erreur sur p2
tu dois trouver
p1 = 1
p2 = ... montre le détail de ton calcul... = 0.3
==> la probabilité p2 qu'il lise le jour n°2 est la somme des probabilités :
- qu'il ait lu le jour 1 et qu'il lise aussi le jour 2
- qu'il n'ait pas lu le jour 1 et qu'il lise le jour 2
ce que je peux écrire ainsi :
de la même façon :
p3 = ... montre le détail de ton calcul... = 0.58
p4 = ... montre le détail de ton calcul... = 0.468
p5 = ... montre le détail de ton calcul... = 0.5128
-c'est Pn barre normalement
je suppose que ceci répond à ma question :
sur la branche Lnbarre, à la place de 0 , tu dois écrire ...? (quelle probabilité en fonction de pn?)
non; attention, pn barre n'a pas de sens mathématique.
ne pas confondre :
- un événement (qui est un ensemble), par ex :
- avec une probabilité (qui est un nombre compris entre 0 et 1) : ici,
d'après le cours sur les événements contraires (ou complémentaires)
si
(regarde comment tu as complété les branches secondaires de ton arbre avec les 0.3 ou 0.7...)
J'avais écrit sur ma calculatrice la suite et cela m'a donnée ces nombres...
Je crois avoir compris, je vais rédiger le début pour commencer
Pour
P(Ln barre) = Pn ?
P(Ln barre) = Pn ?
non
cours : soit A un événement de probabilité p
la probabilité de l'événement complémentaire
puisque p(A) + p(
... tu le sais ! puisque tu l'as déjà utilisé pour calculer les 0.7 et 0.3 de tes branches secondaires
donc
si pn est la probabilité de l'événement Ln,
alors la proba de l'événement
On sait que P3 =p(L2 L3)
L3)
+p(L2 barre  L3)
L3)
Mais on ne connaît pas ces données ?
On a pu calculer P2 par : p(L1 L2) +p(L1 barre
L2) +p(L1 barre  L2)
L2)
=0,3
Si j'utilise pn+1 cela fonctionne ?
Soit p3=-0,4*0,3+0,7
=0,58
on sait que p1 = 1
à l'aide de l'arbre :
p2 = p(L2) = p(L1 L2) +p(L1 barre
L2) +p(L1 barre  L2) = 1*0.3 + 0*0.7 = 0,3
L2) = 1*0.3 + 0*0.7 = 0,3
et donc p(L2barre) = 1-0.3 = 0.7
de la même façon, p3= p(L2 L3) +p(L2 barre
L3) +p(L2 barre  L3) = 0.3 *0,3 + 0,7 *0.7 =0,58
L3) = 0.3 *0,3 + 0,7 *0.7 =0,58
on peut continuer ainsi, mais on peut déjà calculer
p2 - p1 = 0.3-1 = -0.7
p3 - p2 = 0.58-0.3 = 0.28  -0.7
-0.7
on constate que la différence entre 2 termes consécutifs de la suite (pn) n'est pas une constante, quel que soit n N
N
ce contre exemple suffit à montrer que la suite n'est pas arithmétique (d'après la définition d'une suite arithmétique, cf cours)
pour montrer qu'elle n'est pas géométrique, on peut calculer les rapports :
p2 / p1 = .....
p3 / p2 = .....
et en conclure ....?
ceci est une méthode pour montrer que la suite (pn) n'est ni arithmétique ni géométrique sur N.
autre façon, sans doute plus appropriée à l'énoncé :
au début de la question 2) tu as établi (ou tu vas établir...) que, pour tout n N, on a :
N, on a :
pn+1 = -0,4pn + 0.7
==> regarde, dans le cours, la forme récurrente d'une suite arithmétique ?
à quoi la reconnait-on ?
pourquoi peut-on affirmer que la suite (pn) n'est pas arithmétique ?
regarde, dans le cours, la forme récurrente d'une suite géométrique ?
à quoi la reconnait-on ?
pourquoi peut-on affirmer que la suite (pn) n'est pas géométrique ?
+
Pn+1=(0,3*pn)+((1-pn)*0,7)
Pn+1=0,3pn+0,7-0,7pn
Pn+1=-0,4pn+0,7
parfait
2)
Pour démontrer que vn+1= - 0,4pn+0,2
Il faut remplacer dans l'expression vn=pn-0,5, pn ?
J'avais ainsi dit que pn=-0,4(n-1)+0,7 était incorrect mais pn=-0,4(pn-1)+0,7 c'est correct ?
pn=-0,4(pn-1)+0,7 c'est correct ?
fais plus simple
3)on définit pour tout n appartenant à N la suite (vn) par vn=pn - 0,5
Montrer que vn+1=-0,4pn+0,2 --- on demande vn+1
on sait que vn = pn - 0,5
donc vn+1 = pn+1 - 0,5
or, en 2), on a établi que pn+1 = -0,4pn + 0.7
donc
vn+1 = ..remplace.... - 0,5
remplace, puis réduis : tu dois retrouver l'énoncé de la question
Très bien merci pour votre aide, il me reste cependant d'autres questions mais je pense pouvoir les réussir par moi même. Cependant, s'il j'ai un blocage je peux reposter ici ?
OK,
Je bloque sur une partie de l'exercice, voici les questions précédentes :
B) exprimez pn en fonction de vn
Pn=vn+0,5
C en déduire que vn+1=-0,4vn
Vn+1=-0 4(vn+0,5)+0,2
Vn+1=-0,4vn
Et he bloque sur donner la nature de la suite,
J'ai essay de faire vn+1/vn
Donc avec vn+1=-0,4pn+0,2 et vn=pn-0,5
Cela me donne
Vn+1/vn=-0,4pn+0,2/pn-0,5
Et je bloque ici :/
3b) exprimez pn en fonction de vn
pn=vn+0,5 exact
3c) en déduire que vn+1=-0,4vn exact
la nature de la suite :
la suite est de la forme (récurrente) : vn+1 = un_nombre * vn
regarde dans le cours, parmi les suites connues...
C'est géométrique vu qu'il y'a un signe multiplié ? Je pensais qu'il fallait faire des calculs pour le démontrer...
Donc la raison est de-0,4
tu as une forme vn+1 = q * vn
cela suffit pour en déduire que la suite est géométrique (par définition d'une suite géométrique).
pour bien l'identifier, tu dois préciser :
- la raison : ici q = -0.4 exact
- ET son premier terme qui est ...?
puis tu peux (cf cours) donner l'expression de son terme général
(peut-être est-ce la question suivante ?)
On ne connaît pas la terme u1, c'est ça qui me dérange un peux pour trouver u0.
Et exacte, la prochaine question est d'exprimer pn et vn en fontion de n

bonjour Stracth47
2 précisions :
- le premier terme d'une suite n'est pas obligatoirement indicé 0.
regarde par exemple la suite (pn) :
son 1er terme est p1=1 (d'où ma question de 10-02-22 à 21:03, souviens-toi)
- pour trouver le 1er terme de la suite (vn) ,
tu vas utiliser la relation de l'énoncé qui définit cette suite, à savoir : vn = pn - 0,5
le 1er terme de la suite (pn) est indicé 1
donc....
ok ?
v1=0,5 donc, et comme q=-0,4 alors v0=0,5+0,4=0,9.
Puisuqe v1=p1-0,5
V1=1-0,5
V1=0,5
e) exprimer vn et on en fonction de n
On a vn=u0-0,4puissnace n
Ou uo=0,9
Pn=vn+0,5
Donc pn=vo+0,5n
?
v1=p1-0,5
V1=1-0,5
v1=0,5 ----- oui
donc, et comme q=-0,4 alors v0=0,5+0,4=0,9. --- 
on est sur suite une géométrique, là.
... et relis mon message précédent..
e) totalement farfelu  (tu t'es lâché ^^)
(tu t'es lâché ^^)
... étudie tranquillou ton cours sur les suites géométriques avant de faire cette question c)
si besoin : ![]() Tout ce qui concerne les suites géométriques
Tout ce qui concerne les suites géométriques
puis reviens faire une proposition sérieuse.
Je le suis précipité effectivement effectivement...
Donc vo=0,5/(-0,4)
Vo=-1,25
Donc vn=vo*q puissance n
Vn=-1,25(-0,4) puissance n
... le premier terme d'une suite n'est pas obligatoirement indicé 0.
v0 n'existe pas puisque p0 n'existe pas
le terme général est donc à corriger (mais attention à l'exposant ! regarde la formule générale dans le cours)
Dans ces cas l'as on peut dire que Vn=v1*q puissance nais dans mon cours il y'a écrit sous la forme explicite : un=uo*q puissance n
cours : terme général d'une suite géométrique : un = up qn-p
en particulier :
- lorsque le 1er terme est indicé 0 : un = u0 qn
- lorsque le 1er terme est indicé 1 : un = u1 qn-1
ceci est à savoir par coeur.
(fais toi une petite fiche récap' pour toutes ces formules essentielles)
mis en application ici: vn = v1 qn-1 = ....?
D'accord merci, mais en soit si on connaît vo on aurait utiliser vn=vo*qn ?
Pour la suite pn désormais, on sait que celui-ci n'était ni géométrique ni arithmétique, mais vn est géométrique...
Donc on peut peut être écrire
Pn=v1*q(n-1)+0,5 n ?
Puisque vn=v1*q(n-1)
mais en soit si on connaît vo on aurait utiliser vn=vo*qn ?
bien sur, si v0 avait été le 1er terme.
ce qui n'est pas le cas dans le cadre de l'exercice.
selon les énoncés, tu dois adapter la formule générale.
pour la suite, progresse dans l'ordre :
vn=v1*q(n-1) ---- puissance n-1
soit
vn = .......?
puis
Pn=v1*q(n-1)+0,5 n d'où provient ce n ?
explique
Je ne sais pas, en faite on ajoute à chaque terme +0,5 a vn je me suis dis que il faut peut être mettre un mais non.
2:
Soit vn=0,5*(-0,4)puissance (n-1)
en faite on ajoute à chaque terme +0,5 a vn je me suis dis que il faut peut être mettre un mais non.

une chance sur deux... perdu (j'ai bien ri!)
allez, on termine :
vn en fonction de n : vn=0,5 *(-0,4)^(n-1)
or (énoncé) vn=pn-0,5
donc pn = vn + 0,5
d'où pn en fonction de n : pn=.....?
puissance n-1 !!
sinon, c'est ça.
remarque : ce genre de suite, de la forme un+1 = a*un + b
est une suite appelée arithmético-géométrique.
et il est fort probable qu'on t'en 'resserve', en DM ou en DS.
donc, à la fin, quand tu as le terme général de la suite,
pense à comparer avec les premiers termes calculés au début :
cela te permet de contrôler si la formule est correcte (pas d'erreur de signes, etc.).
pn=0,5* (-0,4)n-1 + 0,5
pour n = 1 : p1=0,5 * (-0,4)0 + 0,5 = 0.5*(1) + 0.5 = 1 correct
pour n = 2 : p2=0,5 * (-0,4)1 + 0,5 = 0.5*(-0.4) + 0.5 = 0.3 idem
pour n = 3 : p3=...?
Très bien merci pour m'avoir aidé sur l'ensemble du dm. Il reste cependant une dernière question, que je vais faire tout seul, car j'aime pas trop demande de l'aide aux dm mais vu mes connaissances et les bêtises que j'ai sortie  ...
...



