Inscription / Connexion Nouveau Sujet
suites et algorithme
Bonjours, j'aurai vraiment besoin d'aide pour mon DM de maths, je bloque sur deux questions, merci !
Le sujet est le suivant: On considère un triangle ABC isocèle rectangle, tel que AB=AC=cm.
On construit alors des carrés de la manière suivante :
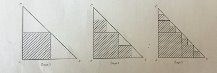
-1ère étape : on construit un premier carré dont trois sommets sont les milieux des côtés du triangle;
-2ème étape : dans les triangles isocèles "restant", on construit des carrés selon le même principe;
-...
-n-ième étape : on construit selon le même principe.
( un schéma est à la fin de l'exercice)
On note Un l'aire hachurée, en cm², obtenue lors de l'étape n.
1. Calculer U1, U2 et U3
2. (a) Quel est le nombre de carrés ajoutés lorsqu'on passe de l'étape n à l'étape (n+1)
(b) Quel est la largeur des carrés ajoutés lorsqu'on passe de l'étape n à l'étape (n+1)
(c) En déduire que pour tout entier naturel n : Un+1/2n JE BLOQUE SUR CETTE QUESTION c !!
(d) Déterminer alors le sens de variation de la suite (Un).
(e) Justifiez à l'aide d'un argument géométrique, que pour tout entier naturel n : Un < 2.
3. On considère l'algorithme suivant :
Variables : N et I sont des entiers, U et C sont des réels
Entrée : Demander à l'utilisateur la valeur de N
Traitement: Affecter à U la valeur 1
Pour I allant de 1 à N-1
Affecter à C la valeur 1/2I
Affecter à U la valeur U +C
Fin de Pour
Sortie : Afficher la valeur de U
(a) Faire fonctionner cet algorithme lorsque l'utilisateur entre N=4. Quel est le rôle de cet algorithme ?
(b) Modifier cet algorithme pour qu'il affiche au bout de combien d'étapes l'aire restante (l'aire du triangle ABC moins l'aire hachurée) sera inférieur à 0.1mm² JE BLOQUE SUR CETTE QUESTION b !!
Merci d'avances aux personnes qui m'aideront !
Bonjour ,
moi aussi je bloque car je pense qu'il manque quelque chose dans ton énoncé
(c) En déduire que pour tout entier naturel n : Un+1/2n
Cordialement
Bah justement c'est pour cela que je n'arrive pas à le déduire, je pense qu'il faut utiliser les 2 questions d'avant et expliquer et non démontrer mais je n'arrive pas
Le problème c'est qu'on ne sait pas ce qu'il faut déduire .
Il faudrait avoir quelque chose comme
"en déduire que pour tout entier naturel n : .... = ...."
Est-ce que la question ne serait pas plutôt :
"en déduire que pour tout entier naturel n : Un = Un-1 +
J'ai trouvé pour la a qu'on ajoute le double de carré qui ont été ajoutés à l'étape précédente et pour la b que la largeur des carrés ajoutés est la moitié de ceux ajoutés à l'étape précédente
J'arrive donc à justifier que Un+1 = Un mais c'est l'exposant de 1/2 qui m'embête parce que j'ai compris pourquoi il etait là mais je n'arrive pas à justifier
Parce que piur la première question j'avais procédé de cette facon pour U2 par exemple =
U2 = U1 + (1/2)2 x 2
J'arrive donc à justifier que Un+1 = Un
L'énoncé comporte encore des manques .
On considère un triangle ABC isocèle rectangle, tel que AB=AC=cm.
As-tu calculé U1 ? , U2 ? U3 ? C'est ce qui est demandé en premier .
Non ce que j'ai voulu dire c'est quand la formule que je dois justifié j'arrive à justifier le début (soit Un+1 = Un) mais pas la suite (+1/2n)
Et oui j'ai calculé U1,U2 et U3
C'est 2 cm, excusez moi pour les fautes ou oublis de frappes dans l'enoncé
Maintenant que l'énoncé est complet (j'espère) , on peut avancer plus sérieusement .
Et oui j'ai calculé U1,U2 et U3
Et donc U1 = ???
U2 =
U3 =
Ensuite il faut répondre à 2-a) et 2-b) .
Alors j'ai considéré que la suite démarrait de U1, je n'aurai peut être pas du car comme ce n'était pas précisé dans l'énoncé, je ne savais pas vraiment quoi faire
Allrs pour U1, j'ai trouvé 1cm2, pour U2: 1,5 et pour U3 = 1,75
Pour la réponse 2/A
J'ai trouvé qu'on ajoutera dans l'étape (n+1) le double de carré qui ont été ajoutés à l'étape n
Pour la réponse 2/b
J'ai trouvé que la largeur des carrés ajoutés lorsque l'on passe de l'étape n à l'étape (n+1) est la moitié de ceux ajoutés à l'étape n
Tes réponses sont juste mais une présentation sous forme de tableau permet de mieux entrevoir l'évolution . La suite peut très bien démarrer à 1 .
| n | U | |
| 1 | 1 | |
| 2 | 1 + 1/2 | |
| 3 | 1 + 1/2 + 1/4 |
| n | 1 + 1/2 + 1/4 + ... + 1/2(n-1) | |
| n+1 | Un + 1/2 n |
| n | nb. de carrés ajoutés | largeur carré | aire ajoutée | ||
| 1 | 1 | 1 | 1 | ||
| 2 | 2 | 1/2 | 1/2 | ||
| 3 | 4 | 1/4 | 1/4 | ||
| 4 | 8 | 1/8 | 1/8 | ||
| 5 | 16 | 1/16 | 1/16 | ||
| n | 2(n-1) | 1/2(n-1) | 1/2(n-1) | ||
| n+1 | 2n | 1/2n | 1/2n |
Donc , l'aire grisée au niveau n+1 étant égale à l'aire grisée au niveau n plus l'aire ajoutée au niveau n+1 :
Un+1 = Un + 1/2n
Je croyais que tu avais compris .
Tu as la réponse dans mes tableaux .
L'aire au niveau n est égale à l'aire au niveau n-1 plus l'aire ajoutée au niveau n donc:
Un = Un-1 + 1/2n-1


