Bonjour! Voici un exercice qui m'a posé du fils à retordre et j'ai l'impression d'avoir fait n'importe quoi... Pouvez-vous m'indiquer si mon raisonnement et correct et où sont mes erreurs...

On considère le triangle ABC dans un repère (O; vec i, vec j). Le point C a pour coordonnées (5/2;−4). Le but de l'exercice est de déterminer s'il existe une fonction polynôme du troisième degré dont la courbe passe par les points A et B et dont les tangentes en A et en B sont respectivement les droites (AB) et (BC).

1. Soit f(x)=ax^3+bx^2+cx+d où a,b,c et d sont quatre réels avec a≠0.
a. Exprimer en fonction de a,b,c et d les images f(1) et f(3).
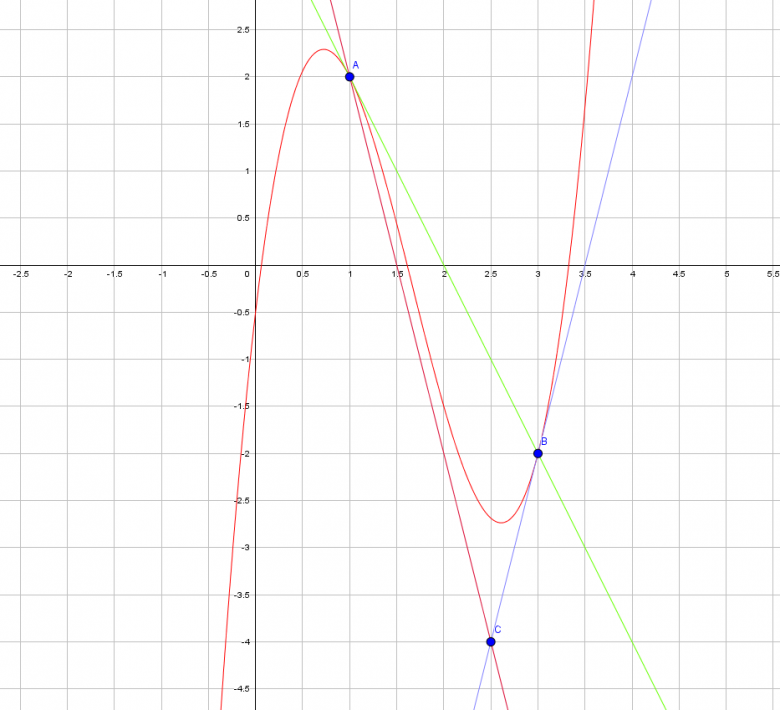
b. À l'aide du graphique, en déduire deux équations d'inconnues a,b,c et d.

2.
a. Déterminer la fonction dérivée de f et exprimer f′(1) et f′(3) en fonction de a, b et c.
b. À l'aide du graphique, en déduire deux nouvelles équations d'inconnues a,b,c et d.

3.
Résoudre à la calculatrice le système de quatre équations à quatre inconnues obtenu aux questions précédentes.

4.
Conclure.

Mes avancées :

1. a) f(1) = a(1)^3 + b(1)^2 + c(1) + d = a + b + c + d

f(3) = a(3)^3 + b(3)^2 + c(3) + d = 27a + 9b + 3c + d

Donc, f(1) s'exprime comme a + b + c + d et f(3) s'exprime comme 27a + 9b + 3c + d en fonction de a, b, c et d.

b) Soit f(x) = ax^3 + bx^2 + cx + d la fonction polynôme cherchée. On a les informations suivantes :

f(1) = 2 (car le point A a pour coordonnées (1,2))
f(3) = -2 (car le point B a pour coordonnées (3,-2))
La tangente à la courbe de f(x) en A est la droite (AB)
La tangente à la courbe de f(x) en B est la droite (BC)
La pente de la tangente à la courbe de f(x) en A est égale à la pente de la droite (AB), qui est (yB - yA)/(xB - xA) = (-2 - 2)/(3 - 1) = -2. Donc, on a :

f'(1) = 3a + 2b + c = -2

De même, la pente de la tangente à la courbe de f(x) en B est égale à la pente de la droite (BC), qui est (yC - yB)/(xC - xB) = (-4 - (-2))/(5/2 - 3) = -4/7. Donc, on a :

f'(3) = 27a + 6b + c = -4/7

Enfin, comme la courbe de f(x) passe par les points A et B, on a :

f(1) = 2
f(3) = -2

Nous avons donc un système de trois équations à trois inconnues :

3a + 2b + c = -2
27a + 6b + c = -4/7
a + b + c + d = 2
27a + 9b + 3c + d = -2

On peut résoudre ce système d'équations pour trouver les valeurs de a, b, c et d. En effectuant les opérations nécessaires, on trouve :

a = 1/7
b = -9/7
c = 16/7
d = 2

Ainsi, la fonction polynôme cherchée est f(x) = (1/7)x^3 - (9/7)x^2 + (16/7)x + 2.

2. a)
La fonction f(x) est donnée par f(x) = ax^3 + bx^2 + cx + d, où a, b, c et d sont des constantes. Pour déterminer la fonction dérivée de f(x), on doit calculer f'(x), qui est donnée par :

f'(x) = 3ax^2 + 2bx + c

Ainsi, f'(1) est donnée par :

f'(1) = 3a(1)^2 + 2b(1) + c = 3a + 2b + c

Et f'(3) est donnée par :

f'(3) = 3a(3)^2 + 2b(3) + c = 27a + 6b + c

En remplaçant les valeurs de a, b et c trouvées dans la question précédente, on obtient :

f'(1) = 3a + 2b + c = 3(1/7) + 2(-9/7) + (16/7) = -2

f'(3) = 27a + 6b + c = 27(1/7) + 6(-9/7) + (16/7) = -4/7

Ainsi, on a f'(1) = -2 et f'(3) = -4/7 en fonction de a, b et c.

b)
À partir du graphique, on peut déduire deux informations supplémentaires :

La courbe de f(x) passe par le point C, qui a pour coordonnées (5/2,-4)
La tangente à la courbe de f(x) en C est la droite parallèle à la droite (AB)
La pente de la droite (AB) est :

(yB - yA)/(xB - xA) = (-2 - 2)/(3 - 1) = -2

Donc la tangente à la courbe de f(x) en C a également une pente de -2. La pente de cette tangente est donnée par la dérivée de f(x) en C, qui est :

f'(5/2) = 3a(5/2)^2 + 2b(5/2) + c = -2

En résolvant cette équation pour c, on a :

c = -15a - 5b - 4

De plus, comme la courbe de f(x) passe par le point C, on a :

f(5/2) = -4

En utilisant la fonction f(x) et la valeur de c trouvée ci-dessus, on a :

f(5/2) = a(5/2)^3 + b(5/2)^2 + c(5/2) + d = -4

En remplaçant la valeur de c dans l'équation ci-dessus et en simplifiant, on obtient :

125/8 a + 25/2 b + d = -28/2

Soit :

125/8 a + 25/2 b + d = -14

Nous avons ainsi deux nouvelles équations en a, b, c et d :

c = -15a - 5b - 4

125/8 a + 25/2 b + d = -14

En combinant ces deux équations avec les équations trouvées dans la question précédente, on peut résoudre le système d'équations pour trouver les valeurs de a, b, c et d.

3.
La calculatrice donne la solution suivante :

a = 1/7
b = -9/7
c = 16/7
d = -6

Ainsi, la fonction polynôme f(x) du troisième degré qui passe par les points A et B et dont les tangentes en A et B sont respectivement les droites (AB) et (BC) est :

f(x) = (1/7)x^3 - (9/7)x^2 + (16/7)x - 6

4.
La fonction polynôme f(x) du troisième degré qui passe par les points A et B et dont les tangentes en A et B sont respectivement les droites (AB) et (BC) est :

f(x) = (1/7)x^3 - (9/7)x^2 + (16/7)x - 6

Nous avons donc trouvé une telle fonction polynôme. Cela montre que les conditions données dans l'énoncé peuvent être satisfaites, et que la solution est unique (en admettant que les conditions sont suffisantes pour déterminer une unique fonction polynôme satisfaisant ces conditions).

En conclusion, la réponse à la question posée est oui, il existe une fonction polynôme du troisième degré dont la courbe passe par les points A et B et dont les tangentes en A et en B sont respectivement les droites (AB) et (BC), et la fonction polynôme est donnée par :

f(x) = (1/7)x^3 - (9/7)x^2 + (16/7)x - 6