Encore moi ! (désolé)  Je suis vraiment pas sûr de ce que j'ai fait dans cet exercice...

Énoncé :
Pour tous réels a et b, on définit les réels : M(a,b)= (a+b+∣a−b∣)/2 , m(a,b)= (a+b−∣a−b∣)/2 et S(a)=a/∣a∣(lorsque a≠0).
Partie A
1. Choisir deux nombres réels a et b et calculer M(a,b). Réitérer plusieurs fois le procédé et vérifier que l'on peut conjecturer que M(a,b) donne le maximum entre a et b.
2. On suppose a⩾b. Montrer que M(a,b)=a. Conclure.
3. Choisir a∈R et tracer la courbe représentative de la fonction f définie sur R par f(x)=M(a,x). Qu'observe-t-on ? Pouvait-on prévoir le comportement de f?
Partie B
1. Choisir deux nombres réels a et b et calculer m(a,b). Réitérer plusieurs fois le procédé et conjecturer sur la valeur de m(a,b).
2. Démontrer cette conjecture de la même manière que dans la première partie.
Partie C
Conjecturer et démontrer ce que renvoie la fonction S.

Ce que j'ai fait :

Partie A:

1.+2.
On peut conjecturer que M(a,b) donne le maximum entre a et b en testant plusieurs valeurs de a et b. Par exemple :

Si a = 3 et b = 5, alors M(a,b) = (3 + 5 + |3 - 5|)/2 = (8 + 2)/2 = 5. On remarque que M(a,b) = max(3,5).
Si a = -2 et b = 4, alors M(a,b) = (-2 + 4 + |-2 - 4|)/2 = (2 + 6)/2 = 4. On remarque que M(a,b) = max(-2,4).
Si a = -7 et b = -3, alors M(a,b) = (-7 - 3 + |-7 + 3|)/2 = (-10 + 4)/2 = -3. On remarque que M(a,b) = max(-7,-3).
On peut donc conjecturer que pour tous réels a et b, M(a,b) donne le maximum entre a et b.

Pour le démontrer, on peut utiliser la propriété suivante : |a - b| est égal à a - b si a ⩾ b et à -(a - b) si a < b.

Ainsi, si on suppose que a ⩾ b, on a :

M(a,b) = (a + b + |a - b|)/2 = (a + b + (a - b))/2 = (2a)/2 = a

Donc M(a,b) est égal au maximum entre a et b dans ce cas.

Si on suppose que a < b, on a :

M(a,b) = (a + b + |a - b|)/2 = (a + b - (a - b))/2 = (b +b )/2 =b

Donc M(a,b) est égal au maximum entre a et b dans ce cas aussi.

On conclut que pour tous réels a et b, M(a,b) donne le maximum entre a et b.
3.

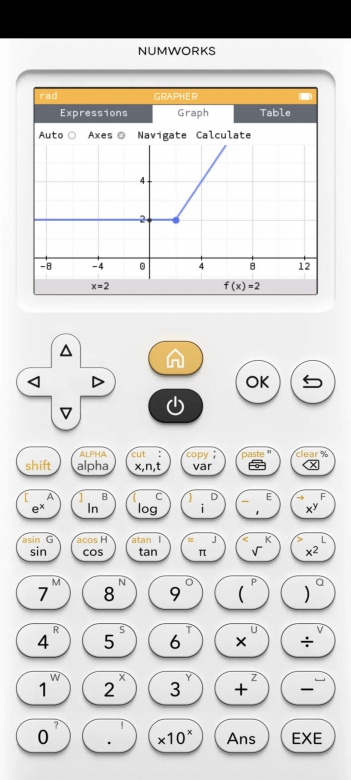
Si a = 2, on obtient la courbe suivante : (voir photo)

On observe que la courbe est formée de deux demi-droites qui se rejoignent au point d'abscisse a. On peut prévoir ce comportement en utilisant le résultat précédent : M(a,x) donne le maximum entre a et x. Donc :

Si x < a, alors M(a,x) = a et f(x) est constante égale à a.
Si x > a, alors M(a,x) = x et f(x) est égale à la fonction identité.
La courbe change donc de pente au point d'abscisse a.

Partie B:

On peut procéder de la même façon que pour M(a,b), mais en utilisant la formule m(a,b) = (a + b - |a - b|)/2. Par exemple :

Si a = 3 et b = 5, alors m(a,b) = (3 + 5 - |3 - 5|)/2 = (8 - 2)/2 = 3. On remarque que m(a,b) = min(3,5).
Si a = -2 et b = 4, alors m(a,b) = (-2 + 4 - |-2 - 4|)/2 = (2 - 6)/2 = -2. On remarque que m(a,b) = min(-2,4).
Si a = -7 et b = -3, alors m(a,b) = (-7 - 3 - |-7 + 3|)/2 = (-10 - 4)/2 = -7. On remarque que m(a,b) = min(-7,-3).
On peut donc conjecturer que pour tous réels a et b, m(a,b) donne le minimum entre a et b.

Pour le démontrer, on peut utiliser la même propriété que pour M(a,b), mais en inversant les signes. Ainsi :

Si a ⩾ b, alors m(a,b) = (a + b - (a - b))/2 = (b +b )/2 =b
Si a < b, alors m(a,b) =(a + b + (a-b))/2 = (a+a )/2 =a
Donc dans tous les cas, m(a,b) donne le minimum entre a et b.

Partie C:

La fonction S est définie par S(a) = a/|a| lorsque a ≠ 0. On peut conjecturer que S(a) renvoie le signe de a. En effet :

Si a > 0, alors |a| = a et S(a) = a/a = 1. Donc S(a) renvoie le signe positif.
Si a < 0, alors |a| = -a et S(a) = a/(-a) = -1. Donc S(a) renvoie le signe négatif.
Pour le démontrer, on peut utiliser la définition de la valeur absolue : |a| est égal à a si a ⩾ 0 et à -a si a < 0. Ainsi :

Si a > 0, alors |a| = a et S(a) = a/a = 1.
Si a < 0, alors |a| = -a et S(a) = a/(-a) = -1.
Donc dans tous les cas, S(a) renvoie le signe de a.