Inscription / Connexion Nouveau Sujet
Tableau de signes/variations fonctions dérivées
 Devoirs33
Devoirs33Bonsoir à tous,
J'aimerai de l'aide pour cet exercice s'il vous plaît. Merci
Exercice 1 :
1) Soit une fonction :
a) Détermine f'(x)
Je trouve f'(x) =
b) Etudier le signe de f.
Ensuite, je calcule le discriminant
, donc admet 2 solutions
Je dresse le tableau de signe :
x | - (-5V21)/2 +
(-5V21)/2 +
f'(x) | - |0| +
c) Dresse le tableau de variation sur [-10;10]
x | - (-5+V21)/2 +
(-5+V21)/2 +
f'(x) | - |0| +
f | qui descend (155-21V21)/12
qui descend (155-21V21)/12  qui monte
qui monte
pour trouver l'extremum, j'ai fait :
f( (-5+V21)/2) = 24 * ((-5+V21)/2) - 5/2 * ((-5+V21)/2)² + 1/3* ((-5+V21)/2)^3
= (155-21V21)/12
2)
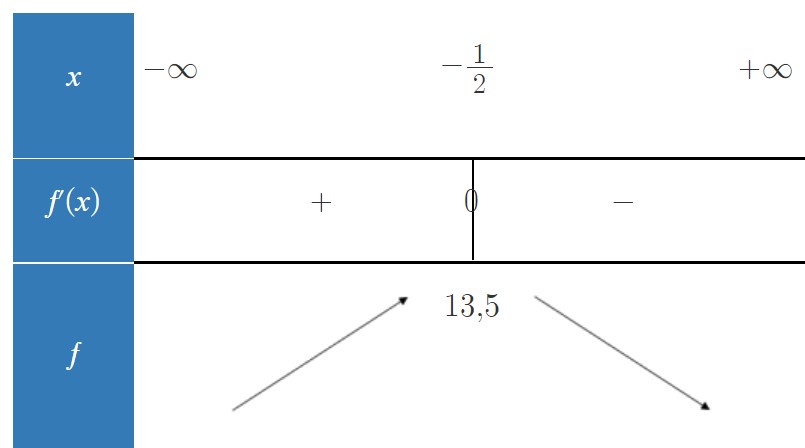
Dresse le tableau de variations de la fonction : f(x) = -6x² - 6x + 12
Je trouve : f'(x) = -12x + 12
3)
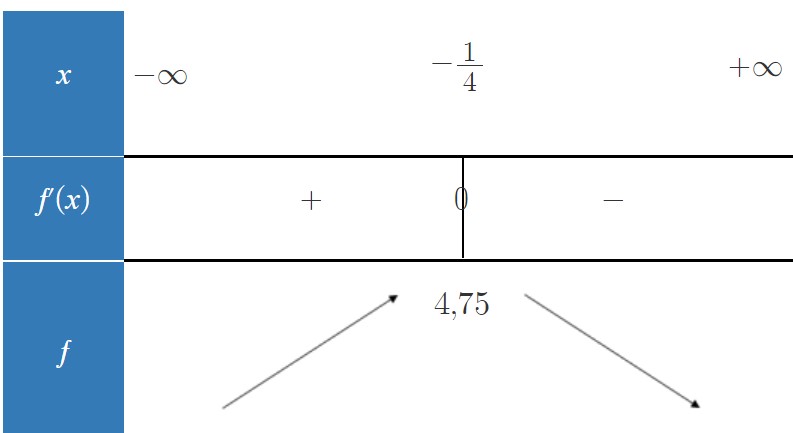
Dresse le tableau de variations de la fonction : f(x) = -4x² - 2x + 4
Je trouve f'(x) = -8x - 2
4)
Dresse le tableau de variations de f(x) = (4x-9)/(4x+8)
Je trouve f'(x) = 68/(4x+8)²
Bonsoir,
Tes 2 premières dérivées sont fausses...
(Attention a bien écrire l'expression de la première fonction  )
)
de passage pour que tu puisses poursuivre
oui, c'est bon, mais prends l'habitude de tout écrire
1) f'(x)=-24 - 5x + x²
D'accord, merci.
1b) Etudier le signe de f' : f'(x)=-24 - 5x + x²
Je calcule le discriminant de f'(x)
 = b² - 4ac
= b² - 4ac
 = 5² - 4*1*(-24) = 121
= 5² - 4*1*(-24) = 121
 > 0, donc admet deux solutions
> 0, donc admet deux solutions
x1 = -b + 
 /2a
/2a
x1 = (5 + 11)/ 2*1
x1 = 8
x2 = -b - 
 /2a
/2a
x2 = (5-11)/2*1 = -3
Dressons le tableau de signes :
x | - -3 8 +
-3 8 +
f'(x) | + |0| - |0| +
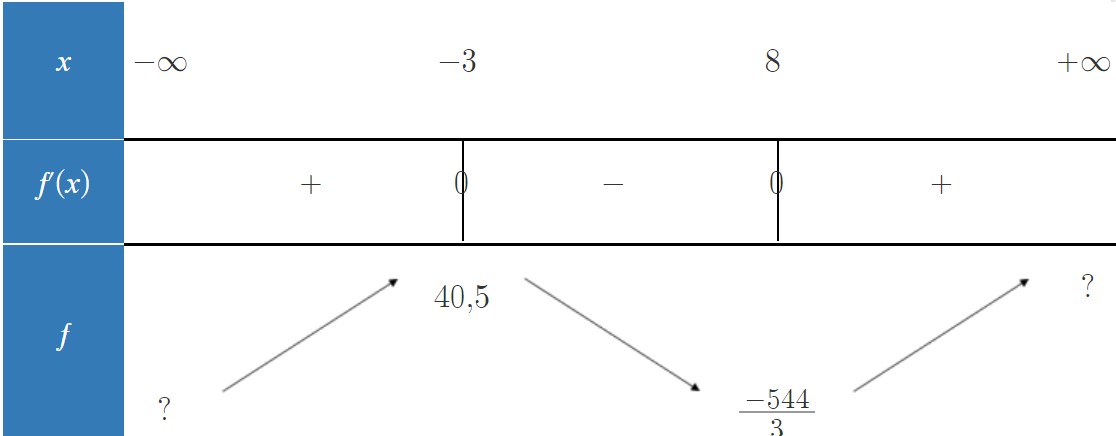
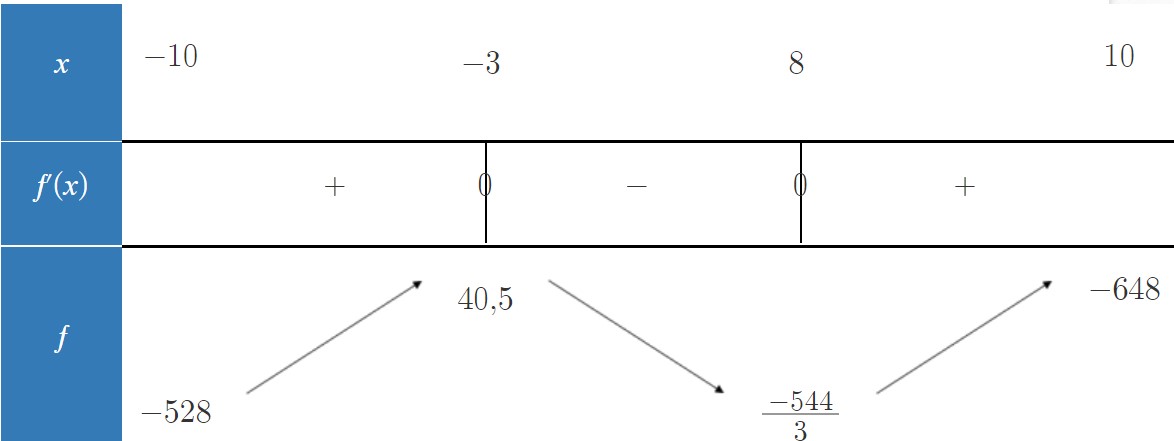
c) Dressons le tableau de variations :
x | - -3 8 +
-3 8 +
f'(x) | + |0| - |0| +
f(x) | qui monte
qui monte  qui descend
qui descend  qui monte
qui monte
Désolée pour le tableau, je n'arrive pas à le faire correctement...
Pour trouver les extremums :
f(-3) = -24*(-3) - (5/2)*(-3)²+(1/3)*(-3)^3
f(-3) = 40,5
f(8) = -24*8 - (5/2)*8² + (1/3)*8^3
f(8) = (-544)/3
?
Merci
arrivée là, tu peux te vérifier rapidement
regarde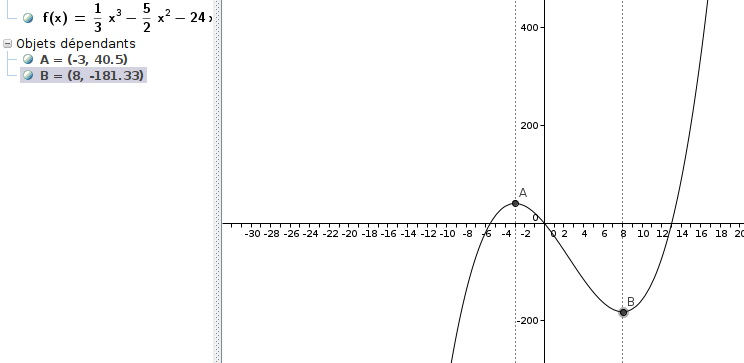
quand tu veux faire un semblant de tableau sur le site, tu peux cliquer sur < / > qui va te bloquer tout ce que tu écris à la place où tu l'écris (faire aperçu pour voir)
ou bien tu utilises l'éditeur Ltx, tableau de variations, avec un peu d'habitude, ça va bien
Bonjour
En l'absence de Foxdevil
D'accord, mais vous oubliez souvent les parenthèses
x1 = -b + 
 /2a se lit
/2a se lit
Vous l'avez bien écrit la ligne d'après
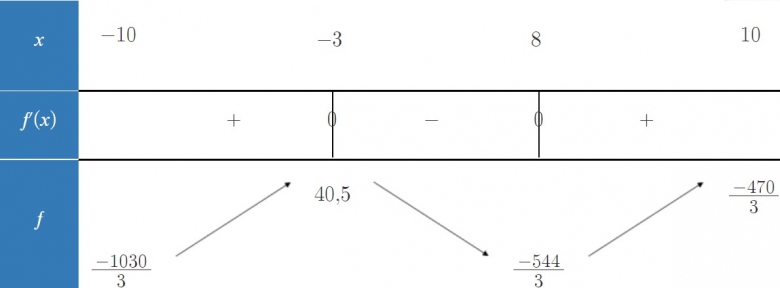
la valeur de f(8) me semble anomale
non non, regarde mon image et la colonne de gauche, tu as la valeur approchée de f(8)
salut,
@Devoirs33
on voit tout de suite que tu sais faire l'exercice.
Tu as juste besoin d'etre rassuree.
Outre les methodes de verfication evoquees ci-dessus,
tu peux egalement proceder ainsi:
On ouvre une session Xcas web (Firefox est recommande mais pas obligatoire) ![]()
On tape successivement:
f(x):=1/3*x^3-5/2*x^2-24x
f'(x)
tabsign(f'(x))
tabvar(f(x),x=-10..10,diff)
graphe(f(x),x=-10..10,display=epaisseur_ligne_2)
voici la session toute prete
Les limites, mais je pense que c'est pour l'année prochaine.
C'est dire ce qu'il se passe lorsque prend des valeurs de plus en plus proche de l'infini
Pour 1c) Je remplace -  et +
et + par -10 et 10 ?
par -10 et 10 ?
Pour 2)
 = -12² - 4*1*6
= -12² - 4*1*6
 = -168
= -168
Donc admet aucune solution
Je voudrai savoir si pour la 1c) je dois remplacer - et +
et + par -10 et 10 ?
par -10 et 10 ?
2) Je trouve f'(x)= -12x - 6
 = (-12)² - 4*1*6 = 120
= (-12)² - 4*1*6 = 120
Donc, admet 2 solutions.
Non justement il n'y a pas de ax²
a=1
mais il m'a dit que a = 1.
Ainsi, je me suis mise à calculer le discriminant
Première question :
f(-10) = -6*(-10)² - 6*(-10)+12 = -528
f(10) = -6 *10²-6*10+12 = -648
Où dois-je rapporter ces valeurs ?
Pourquoi le signe se transforme en
vous savez bien résoudre ce genre d'inéquations
Vous retrouverez les résultats de seconde ou du début de cette année
Oui, donc vous pouvez dresser le tableau de variation
Y a-t-il un ensemble de définition particulier à la place de ?
Pour trouver 4,75, j'ai procédé ainsi :
f(-1/4) = -4*(-1//4)² - 2*(-1/4) + 4 = 4,25
( je me suis trompée, c'est 4,25 au lieu de 4,75)
4) Dresse le tableau de variations de f(x) = (4x-9)/(4x+8)
Je trouve f'(x) = 68/(4x+8)²
Je ne sais pas par quoi commencer. Dois-je utiliser le discriminant ?
On ne parle de discriminant que pour un trinôme du second degré
D'accord pour la dérivée d'ailleurs je vous l'avais déjà dit.
Vous avez une fraction
première question : Quand est-elle définie ?
Valeur à ne pas oublier d'intégrer dans votre tableau.
Que pouvez-vous dire du numérateur ?
du dénominateur ?
du quotient ?



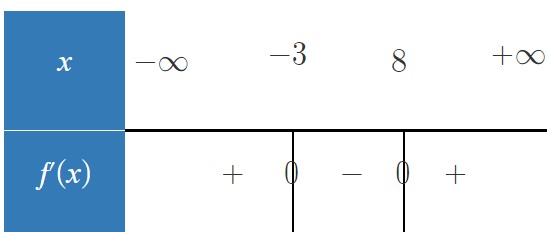

 d'une fraction ?
d'une fraction ?
 0
0
