Inscription / Connexion Nouveau Sujet
Tableau de variation
Bonjour,
Voila j'ai un exercice en math à faire, je l'ai fait mais j'aimerais savoir si j'ai une erreur. Voici le sujet:
Dresser le tableau de variation sur [-4;4]de la fonction f définie par:
f(x)= 3x^4-8x^3-30x²+120x+1
Ce que j'ai fait:
f'(x)= 12x^3-24x²- 60x+120
J'ai fait un tableau de signe
X -4 -
5 2 5 4
en dessous de -4 j'ai 321 puis sous -5 j'ai -78-805 en dessous de 2 j'ai 105 en dessous de 5 j'ai -75+805 et en dessous de 4 j'ai 251
alors de -4 à -5 la fonction est décroissante de -5 à 2 f est croissante puis décroissante et croissante
j'espère que vous comprenez je ne peux pas faire mieux 
merci d'avance.
oui, je vois que tu as trouvé les racines de la dérivée, donc que f '(x)=12x3-24x²- 60x+120 = 12(x-2)(x²-5)
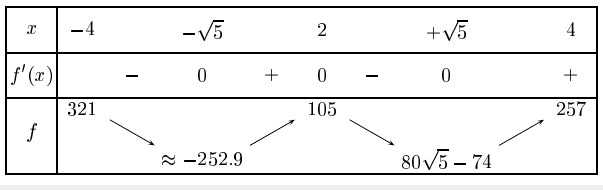
Après, je ne suis pas sûr d'avoir compris tes variations. Tu devrais avoir :
Glapion, j'ai effectivement fait avec la forme factorisé après je me serais trompé pour les valeurs des racines ?
Annuler
connectez vous