Inscription / Connexion Nouveau Sujet
tangente commune à une parabole et une hyperbole
Bonjour, j'ai un problème avec cet exercice :
"On considère la fonction carré f(x)=x² et fonction inverse g(x)=1/x
On note Cf et Cg leurs représentations graphiques respectives dans un repère du plan.
Existe-il des droites tangentes à la fois à Cf et à Cg ?
[...]
Résoudre le problème revient à chercher un réel a et un réel non nul b tels que la tangente à la courbe Cf au point A (a;a²) coïncide avec la tangente à la courbe Cg au point B(b; 1/b)
On montre qu'une équation de la droite Ta est : y= 2ax-a²
On montre ensuite que Ta est tangente à Cg au point B(b;1/b), si et seulement si :
{2a=(-1)/b²
{1/b=2ab-a² "
Logiquement le système comprend pour la première équation les 2 coefficients directeurs des tangentes et la deuxième équation comprend les équations complètes des tangentes. Cependant, je n'arrive pas à trouver 1/b pour l'équation complète de la tangente à Cg ...
Il n'y a pas de difficulté particulière pour trouver l'équation de la tangente à l'hyperbole.
A quelle équation aboutis-tu ?
je n'ai pas le temps là de tout décrire, je pourrai le faire plus tard dans la soirée, mais en gros à un moment donné j'aboutis à 1/b=-1/b+p ...
oui je sais justement je sais calculer aisément le coefficient directeur avec la dérivée, c'est -(1/b²) grâce à un tableau de dérivées usuelles que je connais, et ensuite j'essaie de calculer p avec en gros y= mx+p <=> 1/b = -(1/b²)*b+p <=> 1/b =-(1/b)+p <=> p= 2/b
Donc on a -(1/b²)+2/b  1/b
1/b
On calcule le coefficient directeur de la tangente à l'hyperbole:
g'(b)= -1/b²
Puis on calcule p pour obtenir l'équation complète de la tangente :
y= mx+p <=> 1/b = -(1/b²)*b+p <=> 1/b =-(1/b)+p <=> p= 2/b
J'ai donc une tangente qui a pour équation -1/b²+2/b (peut-être simplifiable) mais ça ne correspond pas du tout à ce qui est demandé...
Alors, puisqu'on a m = - 1/b² et p = 2/b, l'équation de la tangente est y = (-1/b²)x + 2/b .
Rapproche-la de l'équation de la tangente à la parabole au point d'abscisse a et écris que les deux équations sont identiques.
bonjour Priam,
tu aurais même dû mettre en rouge et en gras le "y = " et le "x" dans l'équation de la tangente, car extherion persiste à croire que "-1/b² + 2/b" serait une équation d'une droite !!! (tangente ou pas ce n'est même pas une équation)
Merci bien mais en fait il suffisait de dire que l'ordonnée de b vérifiait l'équation de Ta, donc ce que j'ai fait ne servait en fait à rien...
Enfin je me comprends 
le problème n'est pas que tu te comprennes, mais que ta rédaction soit claire et rigoureuse vu du lecteur/correcteur.
Si tu es le seul à comprendre ce que tu as écrit cela veut dire que ce que tu as écrit est tout simplement considéré comme faux.
Ecrire une droite comme tu l'as écrit c'est nul.
Et non, il ne suffit pas de dire que "l'ordonnée de b vérifie l'équation de Ta" (ce qui encore une fois ne veut rien dire, tu refuses de voir qu'une équation c'est une relation entre DEUX grandeurs, l'abscisse et l'ordonnée)
De plus cela ne prouve qu'une seule chose : la tangente Ta passe par B(b;1/b), pas qu'elle est tangente en B(b;1/b) à l'hyperbole. Toi tu considères que du moment quelle coupe l'hyperbole c'est qu'elle est tangente... bein voyons.
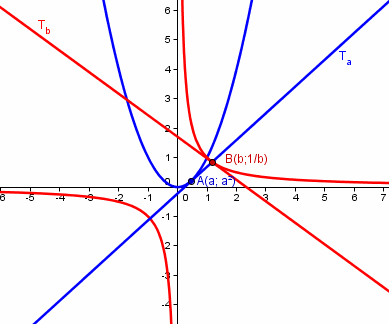
Ici B est bien sur la tangente Ta, les coordonnées de B vérifient bien l'équation de Ta. Et alors ??? c'est pas ce qu'on demande !! On cherche les points A et B pour lesquels Ta et Tb sont la même droite, pas deux droites différentes...
La bonne méthode c'est comme a dit Priam :
écrire l'équation de la tangente en A
écrire l'équation de la tangente en B
écrire que ces deux équations représentent la même droite.
c'est à dire que leurs coéficients sont égaux.
y = max + pa équation de la tangente en A à la parabole
y = mbx + pb équation de la tangente en B à l'hyperbole
Les deux équations représentent la même droite si et seulement si :
ma = mb
et pa = pb
système qui est celui mentionné dans l'énoncé
sur ce je dois te quitter.


