salut
oui il n'y a qu'une tangente car le coeff directeur de cette tangente est f'(a) or f'(x) est une fonction , ce qui signifie que pour un x tu as un seul f'(x) possible...donc tu as un seul f'(a) possible donc un seul coeff directeur

Bonjour,

Une courbe peut très bien avoir deux tangentes en un même point mais alors :
soit c'est un point anguleux (on parle alors de "demi-tangentes") la fonction f(x) dont cette courbe est la courbe représentative n'est alors pas dérivable en ce point
exemple : f(x) = valeur absolue de (x²-1)



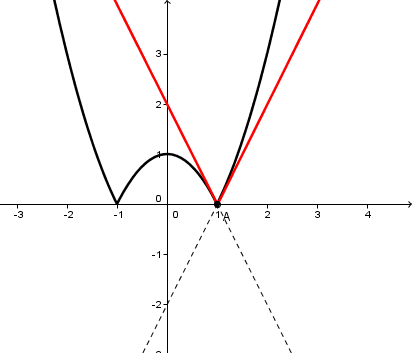
soit c'est carrément un point d'auto-intersection (la courbe se recoupe elle-même) ce qui lui interdit d'être la courbe représentative d'une fonction y = f(x) :
à chaque valeur de x du domaine de définition doit correspondre une et une seule valeur de y (et donc partout où elle est dérivable une et une seule valeur de f '(x))

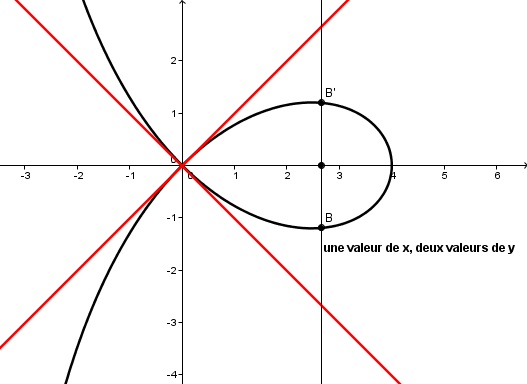
Bonjour ;

C'est une question émanant d'un futur grand mathématicien : Bravo !

Pour essayer d'approcher une réponse à votre question , on va définir d'abord un autre objet mathématique : La droite sécante.
Une droite est sécante à une courbe lorsqu'elle la coupe en au moins un point .

Pour un point P donné d'une courbe, on va considérer les sécantes issues de ce point et qui coupent la courbe en d'autres points différents de P.

La tangente à la courbe au point P est la limite , quand elle existe , des droites sécantes issues de P lorsque le deuxième point Q se rapproche de P le long de la courbe .

Et du fait que c'est une limite, donc elle est unique.

Une remarque : il existe un voisinage de P où la tangente à la courbe au point P n'admet qu'un seul point de rencontre avec la courbe, mais il se peut que cette tangente coupe la courbe en un autre point en dehors de ce voisinage.

Merci infiniment à ciocciu, mathafou et aymanemaysae!

Voilà qui est très clair et qui devra vraisemblablement clore le débat sur cette question.

bien cordialement

merci à mathafou pour son complément , moi je traitais seulement le cas où f dérivable