Inscription / Connexion Nouveau Sujet
Tangentes et nombres dérivés
Bonjour je dois faire un exercice pourriez vous m'aider svp
Dans le repère orthonormé (0;I,j ) ci-contre, la courbe rouge Cf , représente une fonction f définie et dérivable sur IR, les droites tracées en bleu représentent les tangentes à Cf, respectivement au point O, au point B d'abscisse 1 et au point C d'abscisse
3.
1. Déterminer graphiquement
f'(0), f'(1) et f'(3).
2. Déterminer l'équation réduite de la tangente à Cf, au point C.
3. La courbe Cf, est la représentation graphique de la fonction
f:x----->x³-4x² + 2x.
Retrouver par le calcul les résultats des questions 1 et 2.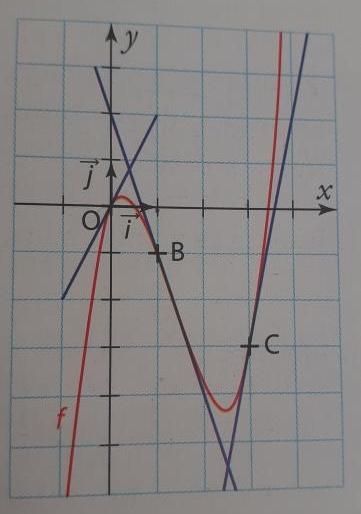
**image tournée**rafraîchir la page**
Bonjour,
1. f '(1) et f '(3) sont justes.
2. Qu'est-ce qui t'embarrasse pour écrire cette équation ?
f'(0) est-il correct ?
et pour m'équation pour ma part j'aurai fais
y= f'(c)*(x-c)+f(c)
mais je suis dans le doute
ou soit y=ax+b
et donc je dois prendre le point b et c
donc B(1;-1)
C(3;-3)
et j'aurai fais yb-ya/xb-xa
pour f'(0)=-4/2 donc -2 je ne comprends pas
et pour l'équation je dois effectuer la premiere proposition que je vous ai faite ou la deuxième
bah je pense qu'il y a deux possibilité parce que la petite droite en bleu on peut lire 4/2 mais de l'autre côté -4/2 mais si vous ditres que c'est juste 2 je vous crois c'est c'est choses dans lequelles je me mélange je ne sais pas comment le s lires et d'accord pour l'équation je la fait et je vous l'envoie
d'accord mais donc que devrais je revoir dans mon equation rempacé x par 3
5x-12
donc cela ferai 5*3-12=3
Pour la 3 je ne sais pas comment procèder
3. La courbe Cf, est la représentation graphique de la fonction
f:x----->x³-4x² + 2x.
Retrouver par le calcul les résultats des questions 1 et 2.
bonjour
en attendant Priam, que je salue et à qui je rendrai la main.
aux questions 1 et 2, on parle de nombres dérivés et de tangente.
... établis la dérivée de f
je viens de regarde un cours: donc j'espère avoir compris on me dit:
x³-4x² + 2x
la dérivé de x³ est 3x
la dérivé de -4x² est -2x1
ce qui fait
3x-2x1+2x
mais je ne suis pas sur pour le -4xcarré
non, ce n'est pas juste; la formule à appliquer est
un exemple d'application, pour concrétiser : dériver x5 - 3x4
et donc
as-tu compris cet exemple ?
si oui, essaie à nouveau ta dérivée
(x³)' = 3*x^(3-1)= 5 x2 -- en rouge, faux
(-4x²)' =-4*2*x^(2-1)=-8x1 = -8x ---- exact, car x^1 s'écrit tout simplement x
2x --- dérivée de ceci ? tu peux appliquer la formule... sachant que x = x^1
reprends
... non tu ne peux pas 
tu peux faire de 2 façons : voir ![]() Formules - Formulaire : Dérivées de fonctions usuelles
Formules - Formulaire : Dérivées de fonctions usuelles
>> soit appliquer directement la formule à apprendre par coeur : (x)' = 1 :
la dérivée de x par rapport à x est 1 ; donc (2x)' = 2*(x)' = 2*1=2
>> mais la formule plus générale de dérivation d'un monôme fonctionne aussi :
==> à retenir : (ax)' = a
j'avance un peu.
lorsque tu auras déterminé l'expression de f '(x),
calcule f'(0), f'(1) et f'(3).
tu dois retrouver les résultats du 1)
puis établis l'équation de la tangente en 3, avec la formule que tu as citée plus haut :
Ta : y= f'(a)*(x-a) + f(a) --- avec a = 3
tu devras retrouver T3 : y=5x-18
3x2-8x+2
et ensuite je dois calculer c'est bien ça ?
MAIS pour le f'(0), f'(1) et f'(3) j'avais déjà trouver avec votre collègue
f'(0)=2, f'(1)=-3 et f'(3)=5
3) Retrouver par le calcul les résultats des questions 1 et 2.
f(x) = x³-4x² + 2x
f '(x) = 3x² -4x +2
en 1) tu as fait une lecture graphique des nombres dérivés, donc tu as fait une conjecture :
en effet, lire sur un graphique comporte toujours des risques d'erreurs liés à la précision du graphique
(épaisseur des traits, grosseurs des points...)
à présent, comme tu disposes de l'expression de la dérivée,
tu peux calculer les images de 0, 1 et 3.
f '(0) = ...
D'accord donc je prends la formule
f '(x) = 3x² -4x +2
Et je remplace les x par pour commencer 0
Ensuite 1 et 3
oups, c'est ma faute, j'avais fait une faute de frappe 
pour punition, je rectifie tes calculs 
f(x) = x³-4x² + 2x
f '(x) = 3x² -8x +2 --- j'avais tapé -4
f '(0) = 3×0² -8×0+2=2 ok
f '(1) = 3×1² -8×1+2=-3
conforme au 1)
question suivante ?
f '(3) = 3×3² -8×3+2= 5
liloudu94226, un petit conseil amical :
prends la bonne habitude d'écrire "y=" ou "f '(x) =" .... quand tu établis une expression ou une équation.
des expressions qui flottent sur la feuille, c'est le meilleur moyen de se mélanger les pinceaux
---
y= f'(3)*(x-3) + f(-3) --- pourquoi -3 ?
la tangente à Cf en 3 s'écrit : T3 : y = f '(3)(x-3) + f(3)
f '(3) = 5
on calcule f(3) = .... calcul de l'image de 3 par f (terminé la lecture graphique, d'accord ?)
d'où
T3 : y = 5(x-3) -3
T3 : y = 5x-18
tu as d'autres questions ?
le règlement du site impose un seul exercice par topic.
ouvre un nouveau topic, avec énoncé, début de tes recherches, et précise où tu bloques.
bonne suite 


