Inscription / Connexion Nouveau Sujet
TD de maths niveau 1èreS
Une pallissade de 2,7m de hauteur est parrallèle à un mur dont elle séparée de 0,1m. Quelle est la longueur minimale d'une échelle qui s'appuie sur le mur et passe par-dessus la palissade?
Normallement, un modèle mathématique nous est donné.
Je vais tenter comme je peux de vous le décrire le plus correctement possible.
O représente le point de contact de la palissade et l'échelle représenté par la droite d.
Il est important de noter que O est un point fixe et que la droite d peut pivoter autour de O.
Le problème est de savoir pour quelle position de la distance AB est minimale (A et B étant les extrémités de l'échelle).
Choisissons un repére orthonormal ds lequel l'équation réduite de d serra la plus simple possible c-à-d un repére de O.
Choisissons aussi une variable en fonction de laquelle nous exprimerons AB.
Nous allons prendre le coeff directeur de d, que ns noterons m. Remarquez que les choix faits impliquent que m est supérieur à O.
Ds le repère, A a pour ordonnée -2,7 et B a pour abscisse 0,1.
1/ Ecrivez des équations de d et de 
, et déduisez-en les coordonnées des points A et B en fonction de m.
2/ Expirmez AB en fonction de m. Posez AB=f(m)
Voila, merci de votre attention. J'éspère que mes inciations sont suffisantes sinon je reste connecter. Merci beaucoup 
Equation de la droite OC (mur) : x = 0,1
Equation de (AB): y = m.x (puisq'elle passe par l'origine du repère).
Coordonnées de B:
B est sur d à l'abscisse 0,1 -> B(0,1 ; 0,1.m)
Equation de (AC): y = -2,7
Coordonnées de A:
A est sur d à l'ordonnée -2,7 -> A(-2,7/m ; -2,7)
Calcul de |AB|²:
|AB|² = (-2,7/m - 0,1)² + (0,1.m + 2,7)²
|AB|² = [(-2,7 - 0,1.m)²/m²] + (0,1.m + 2,7)²
|AB|² = [(7,29 + 0,54.m + 0,01.m²)/m²] + (0,01.m² + 0,54.m + 7,29)
|AB|² = (0,01.m² + 0,54.m + 7,29).(1 + (1/m²))
|AB|² = (0,01.m² + 0,54.m + 7,29).((m²+1)/m²)
AB(m) = V[(0,01.m² + 0,54.m + 7,29).((m²+1)/m²)] avec V pour racine carrée.
Il faut alors trouver la valeur de m qui rend cette fonction minimale avec m dans ]0 ; oo[
Ensuite : Dérivée par rapport à m de AB(m), étude du signe de la dérivée ...
Bon courage si tu veux faire les calculs.
(Remarque: AB² a un minimum au même endroit que AB, et est plus facile d'étudier la fonction donnant AB² ...)
Je suis paresseux et donc je résous graphiquement:
On trouve (graphiquement) que le minimum de AB a lieu pour m = 3.
----------
Autre manière d'aborder le problème.
Autrement:
Les triangles ABC et AOH sont semblables.
OH/BC = AH/AC
2,7/BC = (AC - 0,1)/AC
BC = 2,7.AC/(AC-0,1)
Pythagore dans le triangle ACB:
AB² = AC² + BC²
AB² = AC² + [2,7.AC/(AC-0,1)]²
AB² = AC² [1 + (2,7²/(AC-0,1)²)]
AB est minimum en même temps que AB² ->
en posant AC = x, if faut trouver le min fe
f(x) = x².[1 + (2,7²/(x-0,1)²)]
Il faut de nouveau chercher f '(x) ... -> long
Je résous alors graphiquement:
On trouve le minimun de f(x) pour x = 1.
Soit AC = 1m
--> AH = 0,9 m. il faut poser le pied de l'échelle à 0,9 m de la palissade.
et avec OH = 2,7, on retrouve m = (2,7/0,9) = 3 comme de la première façon.
-----
Sauf distraction.
Si tu dois faire les calculs, bon travail. 
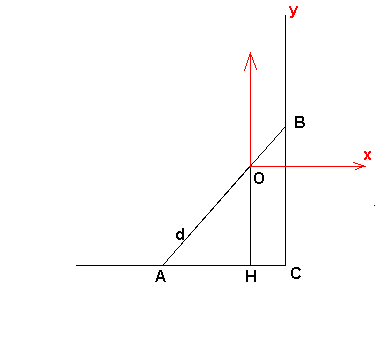
Zut, j'ai mal mis le "y" sur mon dessin de ma réponse précédente, il est bien sûr sur l'axe rouge vertical.
Annuler
connectez vous