Bonjour
Juste pour ne pas me faire oublier
Merci

Bonjour Kader,

1) La loi de   est  Normale(m;) , et non  Normale(117;) (qui est la loi de sous H₀

2a) Le risque de 1° espèce est celui de rejeter H₀ alors qu'elle est vraie ; si H₀ est vraie, alors m=117 , et on la rejette si : le risque de 1° espèce est donc ,   suivant la loi Normale(117;) .

2b) Ici, le risque de 2° espèce visé est celui d'accepter H0 alors que c'est H1 qui est vraie ; dans ce cas m=120, et on accepte H0 si :  le risque de 2° espèce est donc ,   suivant la loi Normale(120;) .

Bonjpour Pierre_D
Merci pour la réponse et j'ai compris quelquechose. cependant j'aimerai poser d'autres questions

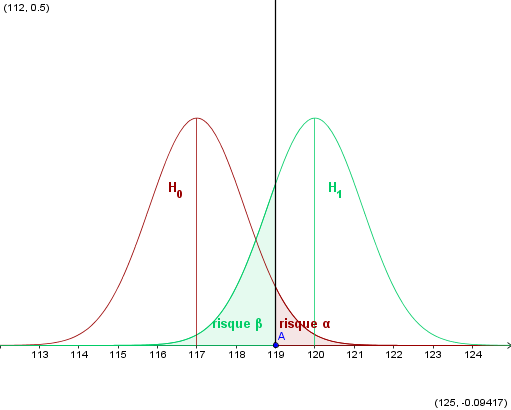
1°) On imagine les courbes en cloche Co sous Ho et C1 sous H1. Est ce que les risques A et B sont toujours l'un à droite, l'autre à gauche sous leurs courbes Co et C1 et ont une frontière commune, la verticale qui est ici 119 ?

2°) Probabilité critique
Voici une définition de la probabilité critique que j'ai relevée sur internet:
Soit T la variable de décision du test et W = [ s, +infini] la région critique.
La probabilité critique du test est c = P(T>t /Ho ) ou' t est l'observation de T

Avec un risque A: si Pc < A, on rejette Ho

Je n'ai rien compris !
Merci pour une aide

Oui

Merci pierre_D pour la réponse.
Ne m'oublie pas pour la probabilité critique si possible
Merci

Si S est la statistique (fonction des résultats de l'expérience, comme un ² observé dans un test de ²) testée sous l'hypothése H0, elle suit une loi de répartition F(S) connue (sous H0) ; si elle prend la valeur s pour les résultats de l'expérience, alors la probabilité que S > s sous l'hypothèse H0 vaut Pc = 1-F(s).
Plus cette probabilité est petite, et plus on aura envie de rejeter H0. En particulier, quand on a fixé a priori un risque de première espèce (seuil de significativité dans l'analyse de variance, par exemple), on rejette H0 si Pc < .

Bonjour Pierre_D

Voici les réponses à l'exercice du début
1°) A=P(X_barre >= 119) sous H0
A=0,05
2°) B=P(X_barre < 119) sous H1
B = 0,205
En passant par la réduction à la loi normale centrée.

3°) Soit n l'effectif pour que B=0,05
P(T < t)= 0,05  T=N(0;1)
(119-120)/(10,5/racine(n)) = t = -1,645
finalement n = 299

4°) Supposons que la moyenne de l'échantillon est 119,5 et on veut calculer la probabilité critique

Dans ta définition, la statistique S est bien la moyenne de l'échantillon, donc
s=119,5
Pc = P(S > s )=P(S>119,5)=0,0196 sous H0   ici S=X_barre
Pc < A donc on rejette H0

Merci de regarder si l'ensemble est correcte ou bien y'a t-il des bêtises

1) et 2) D'accord (écris plutôt A=0,0495)
3) D'accord
4) Et d'accord.
Super !

Bonjour Pierre_D
Merci pour tout. Cependant il y a quelquechose que je ne vois pas bien: Quand on a le risqu A avec son seuil s, est ce que la probabilité critique est utile dans ce cas ? Tout simplement, si me>s on rejette Ho   me = moyenne de l'échantillon

Je pense qu'elle est utile dans le cas ou on a pas calculé s en connaissant A !
Ou est ce qu'il y a une subtilité que je ne vois pas ?
Merci

La probabilité critique permet de savoir à quel risque de première espèce on se situe de façon plus fine qu'en disant seulement < ou > au seuil fixé.
Par exemple, pour un seuil de significativité classique = 0,05 , je serai content de savoir que je suis conduit à rejeter H0 parce que proba(S>s observé) < 0,05 , mais je serai encore plus content de savoir que c'est parce que proba(S>s observé) = 0,0021 , et donc que je n'ai en réalité que 2 chances sur 1000 de rejeter H0 à tort (ce qui est beaucoup mieux que 5 sur 100).

Merci pour la réponse

Je pose pas mal de questions car je ne suis pas scolarisé (j'ai dépassé l'âge) et je fais les mathématiques d'une façon autodidacte.

Malheuresement, les livres et la documentation sur internet ne sont pas assez explicites.

" Justement, dans une documentation sur internet, l'auteur dit ceci:
Le choix des hypotèses Ho et H1 ne doit pas se faire n'importe comment. On privilégie toujours l'hypothèse nulle Ho. Il n'y a qu'à considérer l'exemple du test de l'efficacité d'un médicament..."

Le problème, l'auteur n'explicite pas cet exemple !

Merci

Je ne sais pas ; peut-être veut-il dire que quand on expérimente un médicament nouveau B par rapport à un témoin A, on ne va pas tester une hypothèse H1 = "B diffère de A" contre H0 = "B égale A", mais très probablement une hypothèse H'1 = "B > A" contre H'0 = "BA" (test unilatéral) ?

Bonjour
Soit une population normale (m ; sigma)
Soit X la moyenne des échantillons de taille n
Les livres de BTS donnent :
Si sigma connu : X suit N(m ; s/racine(n) )
Si sigma inconnu : X suit N(m ; s/racine(n-1) )  s=écart type de l'échantillon
                      D'autres donnent  X suit N(m ; s/racine(n/(n-1) )
Sur internet , un auteur donne :  
Si sigma inconnu : Il faut passer par la loi F de Student et il prend cet exemple :
Echantillon : 7 ;9 ;3 ;11 ;10 ;7 ;9 ;12 ;8 ;4
Le problème est de calculer P(X > c ) = 0,05(alpha= 5%) donc un test unilatéral de seuil critique c
moyenne = 8 , s^2 = Somme(xi-s)^2/(n-1) = 8,22  ecart type s=racine(8,22)
c= 6+Finverse(0,95)*s/racine(10) = 6+1,833*racine(8,22/10) = 7,66 ici l'auteur estime sigma par s/racine(n) et le coefficient 1,833 est lu sur la table de Student (qui est donnée pour un test bilatéral je pense),à 9 degrés de liberté, pour un risque de 10% et non pour un risque de 5%  et là, je ne comprends pas

Questions :
1°) Il faut croire Les livres de BTS ou l'auteur cité si dessus ?
2°) La table de Student, est faite que pour un test bilatéral ?

Merci

C'est l'auteur ci-dessus qui a raison :  population où la variable X est normale de moyenne et variance ² inconnues ; échantillon au hasard d'effectif n, donnant les valeurs    de X ;    ;    ;
alors la variable aléatoire      est une variable de Student t à n-1 degrés de liberté.

D'où les intervalles de confiance au niveau 1- pour l'estimation de la moyenne :

- bilatéral :  

- unilatéral "à droite" :  

- unilatéral "à gauche" :  

"La" table de Student donne la valeur du fractile t(,p) de la loi de Student à degrés de liberté  tel que   ; c'est à toi qu'il revient de la lire pour la valeur de p qui te convient (pour le niveau de confiance 1- :  p=1-/2 en bilatéral ,  p=1- en unilatéral) ; dans l'exemple ci-dessus, on cherche un intervalle de confiance unilatéral à droite au niveau 0,95 , et la valeur 1,833 est celle du fractile t tel que .

Merci Pierre_D pour le résumé.
Cependant je n'arrive à lire dans la table de Studen.
P(T9 <= t)=0.95,pour un risque dalpha = 0,05
Dans la table il n y a pas la poraba 0,95
Par contre t=1,833 pour le test unilatéral ci dessus,correspond à la ligne 9 d.l.l ( c'est normal) et à la colonne alpha = 0,10 et cela me laisse penser à 2*0,05=0,10. Alors que dans un test bilatéral on lit à la colonne alpha = 0,05. A moins que pour Student ce n'est pas la même chose que la loi normale centrée ou' de chaque coté cest alpha/2 et peut être que pour Student c'est alpha de chaque côte et cela donne 2*alpha pour un test unilatéral...Je n'en sais rien.
La table que j'ai: alpha 0,90  0,50  0,30  0,20  0,10  0,05  0,02  0,01  0,001 puis la colonne des d.l.l de 1 à 30

il y a un exemple donné: d.l.l=5 et alpha = 0,05, on a l'intersection t=2,571 pour un bilatéral
Merci

Il semble clair que les colonnes de ta table sont des valeurs du risque , et correspondent à une probabilité de   1-/2 (bilatéral) ; je ne trouve pas ça très sain, ni très commode si l'on veut un intervalle de confiance unilatéral au risque : il faut alors aller regarder la valeur de t dans la colonne correspondant à 2, si elle existe ! Dans ta table, cela ne marcherait donc que pour   =  0,01 (colonne 0,02)  ou  0,05 (colonne 0,10)  ou  0,10 (colonne 0,20) ...

Bonjour
J'ai récupéré des tables de Student sur internet et ça va

Sur la calculette TI voici un exemple sur l'intervalle de confiance pour la différence des moyennes de deux échantillons indépendants d'écart type connus
Risque 5% (alpha)
m1=131 ecart type s1=15,5  n1=5
m2=117.4          s2=13,5  n2=5

Résultats de la calculette
IC = [-4,42 ; 31,62]
Marge d'erreur ME = 18.0167

Différence D = (X1_barre - X2_barre)/(racine(s1^2/n1 + s2^2/n2)) suit une loi normale centrée N(0 ; 1)
(131-117,4)/(racine(15,5^2/5 + 13,5^2/5)) = 1,47948
puis je ne sais pas
En plus c'est quoi la marge d'erreur ?

Merci

Les deux échantillons étant indépendants et issus de deux populations où la variable X est normale de variance connue, la différence des deux moyennes estimées fournie par ces échantillons aléatoires,    est une variable normale de variance   = 84,5 ici .

Sous l'hypothèse H0 que les deux populations ont même moyenne,    est alors   . Au niveau de confiance 1- = 0,95 , elle est donc incluse dans l'intervalle bilatéral [-1,960,+1,960] = [-18,017 , +18,017] ici ; il suffit donc de vérifier l'appartenance ou non de la différence observée (13,6 ici) à cet intervalle pour accepter ou rejeter l'hypothèse H0.

Pour répondre à tes questions sur les résultats de la calculette TI, il semble donc clair que :
- la "marge d'erreur ME" est la demi-largeur de l'intervalle de confiance bilatéral (au seuil spécifié) pour la différence des deux moyennes estimées par les échantillons.
- l'intervalle de confiance "IC" qui en découle est curieusement centré sur la valeur observée de cette différence (au lieu de l'être sur 0), ce qui fait qu'il faut regarder, non pas s'il contient cette valeur observée (qu'il contient évidemment), mais s'il contient 0 (la valeur correspondant à l'hypothèse H0) ; je ne trouve pas très heureuse cette façon de faire qui complique la compréhension du test, et préfère la façon dont je l'ai présenté ci-dessus.

Quant à 1,47948 , c'est la valeur de la différence observée après réduction, c'est-à-dire après division par son écart-type    : sa valeur absolue est à comparer directement avec 1,96 , demi-largeur de l'intervalle de confiance au niveau 0,95 de la variable normale réduite.

Bonjour

_{* Tom_Pascal > Un topic = Un exo ! *}

Merci pour une aide

Kader, pour proposer un autre exercice, il faut ouvrir un autre topique ; on te répondra alors dans cet autre topique.