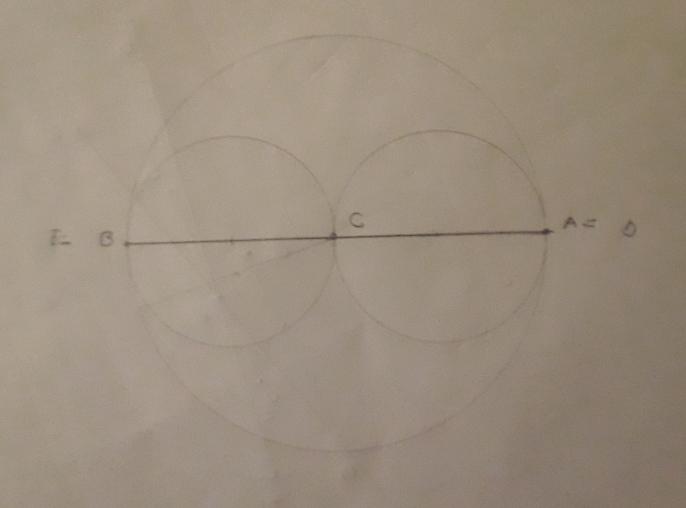
bonjour,

ta figure ne montre pas la généralité de l'énoncé et donc est inutilisable.
(les points D et E y sont confondus avec A et B, ce qu'ils ne sont absolument pas dans le cas général)

les centres des trois cercles n'ont aucune raison d'être alignés,
et donc ne pas faire une figure dans un tel cas bien trop particulier

mais plutôt de ce genre là :

D'accord je comprend dois t-on utilisé les homotheties?

avec un tel titre sans doute (des compositions d'homothéties),
mais honnêtement pour l'instant je ne vois pas comment.

je verrais plutôt une histoire d'angles inscrits ...

Oui je comprend  et si on passait par les rotations genre la rotation de centre c en considérant les deux angles inscrits de même mesure  CAD et CBE

(pour éviter des confusions d'écriture entre le point C et le cercle (C) je renomme le cercle en )
par les homothéties on peut ;

l'homothétie de centre A qui transforme () en (c₁) transforme E en C et la tangente en E à () en la tangente en C à (c₁) etc.

Ou plus simplement le rayon OE en O₁C ...

Puisque l'homothetie conserve l'alignement
L'image de E par l'homothetie de centre A c est C
L'image de O par l'homothetie de centre A est O1  
L'image de D par l'homothetie  de centre  B est C  or C et O1 sont alignés  et C est à la fois l'image de E et D ce qui implique E O et D sont alignés

hum, ...

or C et O1 sont alignés
deux points sont toujours alignés !!

et C est à la fois l'image de E et D
mais par deux homothéties différentes !!

rédaction douteuse donc.

mais il est peut être aussi simple et plus directement compréhensible de dire que l'image (O₁C) d'une droite (OE) est parallèle à cette droite
et idem pour l'autre homothétie. etc

Par l'homothetie de centre A (O1C) parallèle à (EO) ce qui implique que (CO2) parallèle  à ( EO)
L'image de O par l'homothetie  de centre B est O2
L'image (CO2) de ( DO) par l' homothetie de centre  B est parallèle à ( DO)
Donc C O et D alignés

oui.

Merci beaucoup  de votre aide 😊😊