repère orthonormé (A ; AB ; AD)

P (1 ;  tan(a))
Q (tan(pi/4 - a) ; 1)

DQ + BP = tan(a) + tan(pi/4 - a)
PQ²
= (1 - tan(a))² + (1 - tan(pi/4 - a))²
= 2 + tan²(a) + tan²(pi/4 - a) - 2 (tan(a) + tan(pi/4 - a))
= 2 + tan²(a) + tan²(pi/4 - a) - 2 (1 - tan(a) * tan(pi/4 - a))
= [tan(a) + tan(pi/4 - a)]²

la factorisation est très astucieuse merci

Bonjour,

on peut sans calculs :



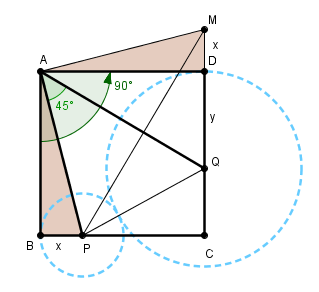
faisons tourner le triangle ABP de 90° autour de A
cela donne le triangle ADM, rectangle en D donc CDM alignés
et avec DM = BP = x
d'autre part AM = AP et l'angle PAM = 90° (la rotation)
PAM est donc rectangle isocèle en A
la bissectrice AQ (45°) est donc en même temps médiatrice de MP
M est donc aussi le symétrique de P par rapport à AQ
par conséquent PQ = MQ = MD + DQ = BP + DQ

nota : par conséquent les cercles de centre P de rayon PB et de centre Q de rayon QD sont tangents.
l'angle PAQ de 45° est donc une façon de construire le centre du cercle (Q) étant donné le cercle de centre (P)

mais bon, la géométrie de nos jours ...

Bonsoir,

Une autre démonstration géométrique sans effectuer de rotation :

Ayant construit le carré ABCD et posé un point P sur [BC] :
Traçons le cercle de centre P et de rayon BP et la deuxième tangente AI à ce cercle : PB=PI.
Appelons R l'intersection de la droite (PI) et de la droite (CD).
Considérons alors le triangle IAD : Il est isocèle en A car  AI=AB=AD.
Par construction les angles AIR et ADR dont droits.
Le triangle IRD est donc lui aussi isocèle en R car ses angles sur la base ID sont respectivement complémentaires des angles du triangle IAD donc IR==RD.
Traçons le segment [AR].
Les triangles AIR et ADR sont symétriques par rapport à l'axe (AR) : les angles IAR et DAR sont donc égaux. Immédiatement alors l'angle PAR vaut 45° et le poinr R est le point Q,
On a bien DQ+BP=PQ puisque DQ=IQ er BP=PI .

Joli !!
J'aime bien aussi le sans calcul.