Inscription / Connexion Nouveau Sujet
Triangle circonscrit
Un problème que m'a inspiré celui-ci : 
Le plus grand triangle
Soit un cercle unité centré à l'origine et soit deux points A et B situés sur la tangente horizontale sous le cercle respectivement à une distance de (a+b) et (a-b) de ce point de tangence.
Quelles sont les coordonnées du point C tel que le triangle ABC est circonscrit au cercle?
Il y a une belle solution en s'exprimant avec b et m = a²-b² seulement 
Pour être clair, A = (-a-b;-1) et B = (a-b;-1)
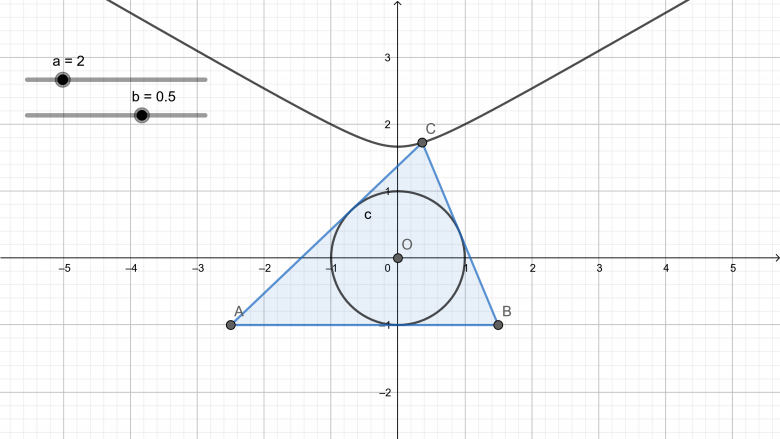
Bonus: En déduire les longueurs de AC et BC. Puis en déduire le périmètre d'un équitriangle (un triangle dont l'aire est égale à la surface, c'est aussi un triangle circonscrit à un cercle de rayon 2).
@dpi
J'ai pris la longue route de mettre le cercle et les droites issues de A et B en équations, de calculer les pentes de ces droites telles qu'il n'y ait qu'une intersection avec le cercle et enfin trouver l'intersection de ces droites.
Après deux pages (j'ai réécris plusieurs fois les étapes car j'ai fait des erreurs) et la vérification des étapes intermédiaires via Géogébra, je suis arrivé à une belle solution.
Il y a probablement une solution via les angles mais je ne suis pas bon en identité trigonométrique et Wolfram Alpha me sort une solution avec des racines partout, pas belle du tout.
J'avais déjà fait à peu près le même calcul . Je n'avais pas calculer les coordonnées du point C mais uniquement la hauteur ce qui donne directement l'aire et donc le périmètre .
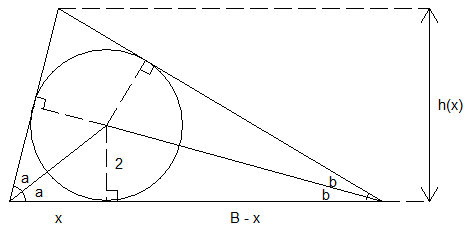
On a : . En faisant varier
entre
et
, la hauteur
va alors décroître de
à
Imod
On ne la fait pas à mathafou 
C'est vraiment simple quand tu le montre comme ça 
J'étais perdu avec mes cotangentes
Comme l'ont montré Imod et mathafou, passer par les coordonnées de C est un détour. Les voici quand même
Cliquez pour afficher@dpi
Ce n'est pas une bêtise, c'est correct
On l'avait montré dans le fil Le plus grand triangle
Une question bête que je pose sans y avoir réfléchi 
On reprend la courbe du point C sur la figure de LittleFox mais avec un cercle de rayon 2 . Tous les points de cette courbe correspondent à des équitriangles ABC . En fait il y a une deuxième courbe symétrique par rapport à l'axe (AB) , on a donc découpé le plan en trois zones . On peut se demander si ces parties permettent de comparer les périmètres et les aires de ABC .
Ca semble vrai pour des raisons de continuité aux passages des frontières.
Après il faut voir si on peut utiliser ça pour finaliser le problème initial .
Imod
J'avais déjà utilisé cette courbe dans le problème initial pour chercher mes meilleurs triangles.
Dans la partie du milieu contenant le segment AB, le cercle inscrit a un rayon inférieur à 2, la surface est donc plus petite que le périmètre. Dans les deux autres, le rayon est suppérieur à 2 et la surface est donc plus grande que le périmètre. Sur la (double) courbe on a l'égalité.
Tout ça vient de r = S/p avec r le rayon du cercle inscrit, S la surface du triangle et p le demi-périmètre du triangle.
D'accord , mais après il faut ajouter le rectangle au canevas et c'est ça qui est intéressant ( on cherche toujours pourquoi deux sommets du triangle maximal sont des sommets du rectangle ) .
Autre chose qui m'intrigue depuis le début , on change complètement le problème en réduisant ou en augmentant les proportions de la figure , on doit pouvoir exploiter cette particularité mais je ne vois vraiment pas comment .
Imod
Une autre observation est que la surface (et le périmètre) est minimale dans le creux de la courbe. Et augmente quand on s'éloigne (|b| grandit).
Une fois A et B posés sur le rectangle, il est facile de voir les intersection de la courbe et du rectangle et de choisir celle la plus éloignée de la médiatrice de AB.
Voici un petit outil Géogébra pour jouer
Annuler
connectez vous