bonjour

pas besoin des angles
fais un petit dessin à main levée,  note x et y les 2 cotés perpendiculaires.

triangles rectangles d'hypoténuse 1 --> déduis-en une relation entre x et y
puis exprime y en fonction de x

périmètre : exprime le périmètre en fonction de x
il te faudra étudier cette fonction pour en trouver son extremum.

Bonjour à tous les deux,
Utiliser des angles ne me semble pas une mauvaise idée
Si a est une mesure d'un des angles non droits, le périmètre est cos a + sin a + 1 .
Il s'agit donc de trouver le maximum de cos a + sin a .
Cette somme peut s'écrire avec un seul cosinus.

Bonjour,

sait on le faire en première (transformer cos + sin en un seul ?)
avec Pythagore, on tombe sur une fonction à maximiser qui contient des racines carrées ... bof

autre méthode :
le problème est équivalent à chercher la plus petite hypoténuse pour un triangle rectangle de périmètre donné ...
et là on aboutit au minimum d'un trinôme en deux coups de cuiller à pot.

Bonjour mathafou,
Je ne pense pas qu'on sache le faire systématiquement en première ( transformer une combinaison linéaire de cos et sin en un seul terme ).
Cependant, je ne voulais pas que louis51 pense avoir eu une idée farfelue.
Est-ce plus difficile en première de trouver comment transformer cos a + sin a qu'envisager, comprendre, justifier et terminer la méthode que tu proposes ?

Autre question pédagogique : Sait-on en première dériver u quand la fonction u n'est pas affine ?

ma méthode "rapide" consiste à comprendre que

trouver le maximum de A, B étant donné
est totalement équivalent à trouver le minimum de B, A étant donné

(intuitivement évident, et si on veut une justification formelle, on passe par la définition de fonctions croissantes et décroissantes)

et ce quelles que soient les significations de A et de B (ici périmètre et hypoténuse)

il est bien plus facile de substituer y depuis P = x+y+1 dans d² = x²+y² que le contraire
donc en retournant le problème ainsi on obtient des calculs bien plus faciles que le problème direct.

C'est pas plutôt P = x+y+d ?

oui tu as raison.

Je me trompe sans doute, mais je ne trouve pas de "minimum d'un trinôme" ni de "calculs bien plus faciles"

Bonjour,

Si on veut vraiment court-circuiter l' exercice:



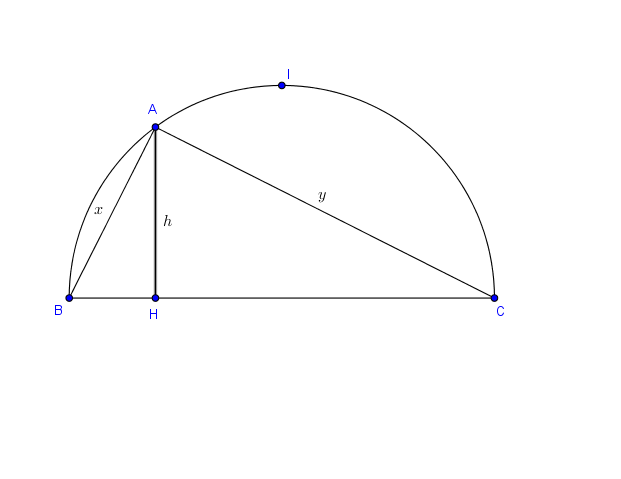
(x+y)^2=BC^2+2xy=1+2xy

Et x+y est maximum lorsque xy=AH.BC=AH l' est, donc lorsque A est en I milieu de l' arc.

Bonjour lake ,
Joli le demi-cercle et xy = AH
Moins élégant :
On peut commencer par faire une conjecture à l'aide d'un logiciel de géométrie dynamique.
On va trouver que le périmètre maximum semble être 1+2 quand le triangle est isocèle.
Reste à le démontrer...

P = 1+ x + (1-x²) où x est la longueur d'un des côtés de l'angle droit.

Le signe de 1+2 - P peut se trouver à l'aide d'une quantité conjuguée puis de la mise en évidence d'une identité remarquable.
Il se confirme alors que ce maximum est atteint pour x = (2) / 2

Le prof qui va corrigé le DM va s'amuser

Oui Sylvieg, quand on sait que cet exercice est en principe une application de la dérivation, nos solutions peuvent paraître "discutables"

Est-il posé uniquement dans ce but ?
Dans mon souvenir, dériver u quand la fonction u n'est pas affine n'était pas au programme en première. Difficile dans ce cas d'utiliser une dérivée.
Je trouve plus satisfaisante une solution qui ne "casse" pas la symétrie entre les deux côtés non connus.

Que pense louis51 de cette avalanche de réponses ?

si on conjecture la symétrie de la solution, on peut avoir intérêt de choisir une mise en équation symétrique

prendre un côté de l'angle droit ou un angle comme "x" est très fortement dissymétrique et entraine les problèmes que l'on a

avec des longueurs et Pythagore
c'est assez affreux mais ne nécessite pas de calculer des dérivées exotiques ni des quantités conjuguées etc



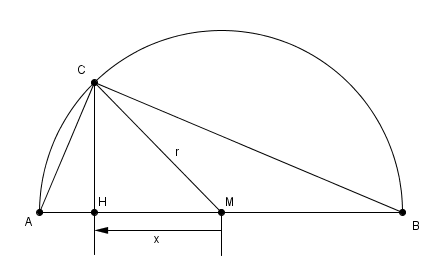
j'appelle r = 1/2 le rayon du cercle circonscrit, pour éviter de se trainer des fractions 1/2 partout
Pythagore donne successivement
dommage je n'écris pas en LaTeX car le serveur LaTeX de l'ile est naze en ce moment (nombreux "can't mkdir cgi/bin" etc)
CH^2 = r^2 - x^2
puis AC^2 = AH^2 + CH^2 = (r-x)^2 + (r^2 -x^2) = 2r^2 - 2rx

de même BC^2 = 2r^2 + 2rx

(AC+BC)^2 = AC^2 + BC^2 + 2.AC.BC = 4r^2 + 2(AC^2.BC^2) = 4r^2 + 2((2r^2)^2 - (2rx)^2) (identités remarquables)
= 4r^2 + 4r(r^2 - x^2)

c'est fini pour les calculs.

passons au raisonnement
P est maximal exactement quand AC+BC est maximal (vu que AB = 1 = constant)
c'est à dire quand (AC+BC)^2 est maximal
c'est à dire quand (r^2 - x^2) est maximal vu que tout le reste est constant
c'est à dire quand r^2 - x^2 est maximal (he he) c'est à dire quand x^2 est minimal, c'est à dire nul (un carré est toujours ≥ 0

et voila comment on résout l'exo au niveau seconde, sans dérivées ni somme de cosinus ni raisonnement sur la dualité des problèmes
bon, il est impossible à un élève d'imaginer une telle démarche s'il n'est pas guidé par des questions intermédiaires ...

ouais ...bof, j'aurais dû regarder la solution de lake

J'ai eu raison d'aller dîner avant de faire une comparaison indélicate

salut

en partant du dessin de lake et en adaptant les notations au niveau considéré si f(x, y) = 1 + x + y est le périmètre

alors f(x, y) = f(y, x) et f est minimale en (0, 1) ou (1, 0) (inégalité triangulaire 1 =< x + y)

donc f(x, x) est maximal par symétrie de la figure par rapport à la médiatrice du segment [AB]


encore avec l'inégalité triangulaire :

h < x + BH
h < y + CH
----------------
2h < x + y + 1

le périmètre est donc maximal lorsque h l'est

...

Bonjour carpediem,
Quelque chose m'échappe dans ta seconde démonstration.
Si je fais le même raisonnement avec x : x < x+y+1 .
On obtiendrait "le périmètre est donc maximal lorsque x l'est"

sauf que x n'est pas une autre grandeur que x ou y

et si x est maximale alors y est minimale et par symétrie ça bogue (puisque le périmètre est en fait minimal)

avec ta remarque il faudrait alors écrire : x < x + y(x) + 1 car y dépend de x

x < x + y + 1
y < x + y + 1
x + y < 2x + 2y + 1 <=> x + y + 1 < 2(x + y + 1) est une tautologie qui ne permet pas de répondre ...

il est clair que le périmètre est plus grand qu'une partie de ce périmètre


moi je minore ce périmètre par une autre grandeur (qui dépend de x et y bien sur)
je montre que ce périmètre est plus grand qu'une autre grandeur (h en l'occurrence qui dépend bien sur de x et y mais qui n'est pas x ni y)
ici A se balade sur un cercle donc il ne faut pas oublier que les variables x et y sont liées : quand x croit y décroit !!!


par contre :

il me suffit que h soit maximale pour avoir un plus grand périmètre ...

il n'est pas dit qu'il n'a pas lieu ailleurs mais la symétrie l'assure car P(x, y) = P(y, x) = x + y + 1

or dP/dx = dP/dy = 1 donc il n'y a pas de points critiques ailleurs

ça ne serait plus vrai si A se baladait sur la courbe de la fonction cos sur l'intervalle [-2pi, 2pi] par exemple avec BC = 4pi

j'avais démontré ce résultat dans un autre post ... mais je ne sais plus lequel ...

pour démontrer cela avec rigueur il faut considérer le système :

P(x, y) = x + y + 1
(sous la contrainte) x^2 + y^2 =1 <=> A appartient au cercle de diamètre [BC]
(et 0 < x < 1 et 0 < y < 1 bien sur)

Merci pour ta réponse.
Franchement je préfère la solution de lake. Elle me semble plus accessible

no problemo ...

cependant ma réponse est exacte et la plus minimaliste

Mais, dans cet exercice, on cherche à maximiser, pas à minimiser

de toute façon la méthode de carpefiel pèche dans son principe à mon avis
il a d'ailleurs bien souligné le problème :
ça ne serait plus vrai si ...

en fait rien ne permet d'affirmer directement que
si P(x, y) est symétrique, on a un maximum "par symétrie" (donc si x = y)

et pire
rien ne permet d'affirmer que si g(x) < f(x) les maxima de l'une sont lies aux maximas de l'autre

illustration :



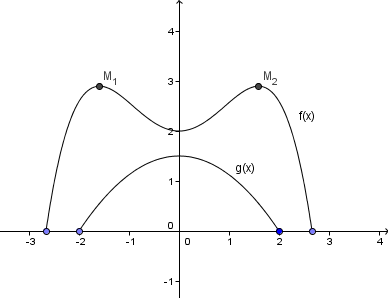
ici "il se trouve" que c'est vrai et le démontrer revient très exactement à faire l'exo (calculer des dérivées etc ou une autre méthode)
donc on ne gagne rien du tout...

Merci mathafou pour cette explication très claire
Je me sentais un peu perdue dans celles de carpediem.

Je ne sais pas pourquoi, ça m'a donné une idée de méthode "calculatoire" qui préserve la symétrie :
Si a et b sont les longueurs des côtés de l'angle droit, on a a² + b² = 1

On peut poser a² = 1/2 + x et b² = 1/2 - x avec -1/2 x 1/2 .

Cela revient à poser x = a² - 1/2 en sachant que 0a²1

Le périmètre est alors 1 + (1/2 + x) + (1/2 - x)

Trouver, avec une dérivée, que son maximum est atteint pour x=0 n'est pas trop compliqué.

il faut encore savoir calculer la dérivée de u

De (ax+b) ; je crois que u(ax+b) est au programme.

Attention, plagiat
1 + (1/2 + x) + (1/2 - x) est maximum quand (1/2 + x) + (1/2 - x) est maximum.

Donc quand le carré de (1/2 + x) + (1/2 - x) est maximum.

Or ( (1/2 + x) + (1/2 - x) )² = 1 + 2(1/4 - x²) .

D'où le maximum pour x = 0 .
Sans dérivées ni somme de cosinus ni raisonnement sur la dualité des problèmes

u(ax + b) est au programme .. mais plus lorsque u est la racine carrée ... du moins pour certaine filière ...

louis51 n'est pas très bavard ; pourtant il y a de la matière...