Inscription / Connexion Nouveau Sujet
triangle inscrit dans une parabole
Bonjour , j'ai un devoir maison a faire et je cherche la méthode pour trouver la réponse à ce problème :
On considère la parabole (p) d'équation y=x2 dans un repère orthonormé . Les points A et B de la parabole (P) ont pour abscisses respectives -1 et 3 . On considère un point M de (P) sur l'arc de parabole AB . Déterminer la position du point M qui rend l'aire de AMB maximale .
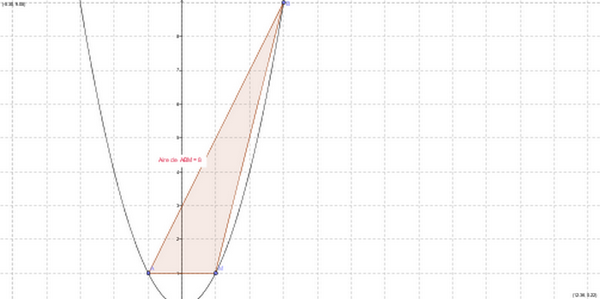
(J'ai déposé si dessous le graphique correpondant)
d'après ce graphique nous pouvons conjecturer que l'aire maximale de AMB est de 8cm2 pour M qui a les valeurs (1.1)
Mais il faut pouvoirs les trouver avec le calcule : j'ai essayé de calculé les longueurs avec : (xb-xa)2+(yb-ya)2)
(xb-xa)2+(yb-ya)2)
mais comme on ne connait pas M cela fait beaucoup d'inconnue . Notre professeur nous a dis qu'on pouvez calculer l'aire mais pas avec la formule basique comme b*h/2 . Mais une méthode spéciale .
Donc si vous avez compris ou connaissez la réponse pouvez vous m'aider, me donner la formule ou des pistes de recherches 
Bonjour,
Bof si, on peut, mais c'est bien plus simple de calculer cette aire comme différences d'aires de trapèzes !!!
il n'y a qu'une seule inconnue : l'abscisse de M
tout le reste est "fonction" de cette abscisse là, ou donné coime valeurs numériques dans l'énoncé.
il n'y a de toute façon aucune longueur à calculer à part les bases (verticales) des trapèzes sus nommés et leur hauteur (horizontales)
et des longuers horizontales ou verticales il n'y a pas besoin de racines carrés pour les calculer !!
je comprends pas l'histoire avec le trapèze ???
Ses vrai que notre professeur nous parlez de trapèze mais je vois encore pas 
Oui, ou pour éviter le cas particulier de AM horizontal ce qu'il n'a aucune raison d'être :
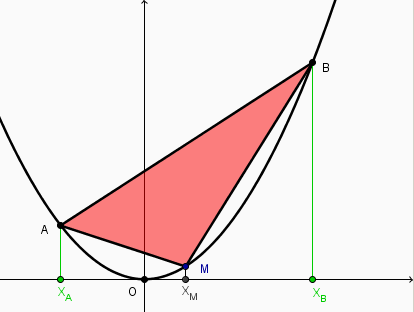
et donc l'aire de AMB = aire du trapèze AXAXBB
moins l'aire des deux trapèzes AXAXMM et MXMXBB
les coordonnées de A et B sont des valeurs numériques qui permettent de calculer la valeur numérique de AXA, BXB et XAXB
les autres s'expriment "en fonction de x", l'abscisse de M
On sait que la parabole (P) a pour équation y=2 donc pour l'ordonné de A y=1 et pour l'ordonné de B y=9
donc l'aire du trapèze AXAXBB : (1+9)*4/2 = 20 cm2
l'aire de AXAXMM : (x+1)*(1+x)/2 = x2+x +1 +x/2
= x2+2x +1 /2
l'aire de MXMXBB :(x+9)*(3-x)/2 = -x2+3x+27-9x/2
= -x2-6x+27/2
l'aire des deux trapèzes AXAXMM et MXMXBB :
x2+2x+1-x2-6x+27/2
est-ce que j'ai bon ou je me suis tromper quelque part 
parce que j'essaie de faire la suite mais sa me donne des résultats pas possible 
http://fr.wikipedia.org/wiki/Aire_d'un_triangle
Coordonnée: A(-1,1) et B(3,9)=> vectAB = (4,8)
=> equation de la droite AB: y-(-1)=(x-(-1))(9-1)/(3-(-1))
<=> y+1 = 2(x+1)
<=> 2x-y+1=0
Posons M(xM,xM2)
comme A et B son fixés donc pour une aire max, la distance entre M et AB doit etre max
d(M,AB)= |2xM - yM +1|/ (22+(-1)2)
(22+(-1)2)
= |2xM -xM2+1|/ 5
5
chercher x pour que |2x-x2+1| soit max =>x=1=> M(1,1)
Quelles sont les dimensions du trapèze AXAXMM, sans sauter d'étapes ?
les bases AXA = 1
et MXM = x² (puisque les coordonnées de M sont (x; x²)
la hauteur = XAXM = x - (-1) = x+1
et donc l'aire = (1 + x²)(x+1)/2 = un truc en x3, normal
il finiront par s'éliminer à la fin ces x3
etc ...
nota :
quand on écrit x2+2x +1 /2
ça veut réellement dire
quels que soient les espaces qu'on a pu mettre la dedans (les espaces ne sont pas un signe mathématique)
pour dire il faut obligatoirement écrire
x2+2x +1
/2 les parenthèses étant absolument obligatoires.
la méthode de chickaboom marche aussi mais c'est plus compliqué (équations de droites, distance d'un point à une droite etc)
marche aussi bien entendu l'utilisation de trucs complètement hors programme comme le calcul du produit vectoriel ou le déterminant d'une matrice ... 
voire même aucun calcul du tout si on connait les propriétés géométriques des paraboles (les milieux de toutes les cordes parallèles à AB sont sur une droite parallèle à l'axe : la médiatrice de XAXB d'ailleurs)
la méthode pour obtenir l'aire de AMB en fonction de x par les trapèzes est, si on ne se mélange pas les pinceaux, bien plus simpole (et "suggérée" par le prof en plus)
quelle que soit la méthode si on se mélange les pinceaux on se casse de toute façon la figure
Oui c'est vrai que j'ai pas compris se que s'est / (22+(-1)2)
(22+(-1)2)
et comment trouver x avec sa formule j'ai pas réussit .
Pour ta méthode sa donne :
AXAXMM = [(1+x2)(x+1)]/2
= (1x +x +x3 +x2)/2
MXBXBB = [(9+x2)(3-x)]/2
= (27 -9x +3x2 -x3)/2
AXAXMM +MXBXB = (4x2-8x +28)/2
Ensuite j'arrive pas a réduire 
à réduire quoi ?
l'aire du triangle est égale à f(x) = 20 - (4x2-8x +28)/2
simple trinome du second degré dont le maximum (parce que le coefficient de x² est <0, c'est donc un maximum) est "comme d'hab" pour x = -b/2a = ...
donc on fait : soit -4x2+8x-28
le sommet de la parabole est -b/2a = -8/2*(-4) = 1
donc x = 1 . a est négatif donc 1 représente le maximum
y= x2
y= 1
Donc pour que l'air ABM soit maximale m doit avoir les valeurs (1.1)
vérifions : 20 - (4x2-8x +28)/2
= 20 -(4*1 - 8*1 +28)/2
= 20 -24/2
= 8 cm2
on retrouve bien les mêmes résultats qu'avec Geogebra 
donc on fait : soit -4x2+8x-28
ça reviendra au même au final mais la fonction n'est pas celle là du tout.
c'est :
f(x) = 20 - (4x2-8x +28)/2 = -2x² + 4x + 6
soyons précis dans la rédaction.
(bon, c'est sûr, maximiser f(x) revient à maximiser -4x2+8x-28 mais si on fait comme ça il faut le dire ce "revient à")
voila. et tu retrouves aussi le résultat donné par chickaboom avec l'autre méthode.
et de façon générale l'abscisse de M sera la moyenne des abscisses de A et B, en plaçant A et B fixés n'importe où.
Cette généralisation ne faisant pas l'objet de l'exo, mais il suffit de remplacer les abscissses données par des valeurs inconnues a et b (paramètres) et le même calcul donne ce résultat