Inscription / Connexion Nouveau Sujet
Triangle rectangle et cercle
Bonsoir, je suis confronté a un petit problème sur un exercice de mon Dm dont voici l'énoncé :
Construire un triangle ABC tel que AB = 6Cm, AC= 10cm et BC= 8 cm
2)Démonter que ABC est un triangle rectangle(C'est fait)
3) On appele E le point du segment [AC] pour lequel AE=1X AC
4
Donc si mes calculs sont exact sa nous donne : 10*1 = 10*1/4= 10/4= 2.5
4
Le cercle de diamètre[AE]Coupe[AB] en F
4)Montrer que le triangle AFE est rectangle
5)Démontrer que les droites(EF) et (BC) sont parallèles
6)Calculer AF et EF
Donc mon problème c'est que je n'options pas de triangle rectangle, pour la questions 4 

Le triangle AFE est inscrit dans
un demi-cercle de diamètre AE
Le triangle AFE est rectangle en F
(EF) et (BF) sont perpendiculaires
à la même droite (AB)
bonjour
4)Montrer que le triangle AFE est rectangle
F est un point du cercle de diamètre [AE].
Si l'on joint un point F d'un cercle aux extrémités A et E d'un diamètre de ce cercle alors l'angle AFE est droit.
Donc l'angle AFE est droit et
la droite (EF) est perpendiculaire à [AB].
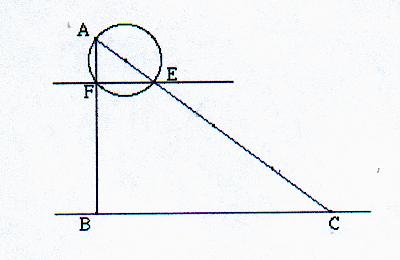
5)Démontrer que les droites(EF) et (BC) sont parallèles
Le triangle ABC est rectangle en B, d'après la question précédente donc la droite (BC) est perpendiculaire à (AB).
Si deux droites sont perpendiculaires à une même troisième droite alors elles sont parallèles.
(EF) perpendiculaire (AB)
(BC) perpendiculaire (AB)
donc les droites (EF) et (BC) sont parallèles
6)Calculer AF et EF
Dans le triangle ABC, (BF) et (CE) sont sécantes en A
(EF) et (BC) sont parallèles
d'après la propriété de Thalès, il y a proportionnalité entre les longueurs respectives des côtés des triangles ABC et AFE
on peut écrire AF/AB = AE/AC = FE/BC
longueur AF :
AF/AB = AE/AC donc
AF/6 = 1/4
AF = 1/4 x 6
AF = 1,5
longueur EF :
FE/BC = AE/AC donc
FE/8 = 1/4
FE = 1/4 x 8
FE = 2
Le segment [AF] mesure 1,5 cm et le segment [FE] mesure 2 cm
A+


