Inscription / Connexion Nouveau Sujet
trouver la fonction f(x) en fonction de x
bonsoir
j'ai besoin d'un coup de mains pour pouvoir continuer mon exercice
alors : on a ABC triangle rectangle en A, tel que AC=3 et AB=4.Le point M décrit le segment [BC] à partir de B.On note x la longueur de BM et f la fonction qui à x associe la longueur de AM,notée f(x).
Et en faite on me demande de trouver le tableau de variation de f en présisant la valeur minimal....)
Donc d'après Phytagore je trouve que BC=5 donc je sais que x appartient forcément a l'intervalle [0;5] puisqu'il appartient a [BC] et je sais aussi que pour x=0 AM=4 et pour x=3 AM=3
mais ensuite je bloque pour trouver la fonction f(x) et donc son tableau de variation avec son minimum..
merci d'avance

oui c'est ce que je voulais dire 
et non je n'ai pas pas encore vu se théorème
en ce moment on est sur les translations de fonction on termine mais je doute que l'exercice porte sur cela je pense que la fontion doit ètre un polynome du second degrès ou bien un fonction carré ou bien une autr fonction .....
bonjour
soit N le projeté de M sur AB
thales => MN/x = 3/5 => MN=3x/5
dans ANM => AN²+MN²=y²=> AN²=y²-9x²/25
or MN²+NB²=x² => NB²=x²-9x²/25 = (4x/5)²
or AN+NB=4 V(y²-(3x/5)²)+4x/5 = 4
y²-(3x/5)² = (4-4x/5)²
y=V(25x²-160x+400)/5 car y >0
Vérifies...
Philoux
ok  ,
,
j'ai peut-être une idée
essaie de voir ainsi (je pense que cela fonctionne  )
)
soit H le projeté orthogonale de M sur [AB]
et K celui sur [AC]
essaie de trouver les longueurs Mk et MH en fonction de x (utilise tes formules de trigo pour le faire)
ensuite, tu devrais arriver à trouver AM avec le th. de Pythagore 
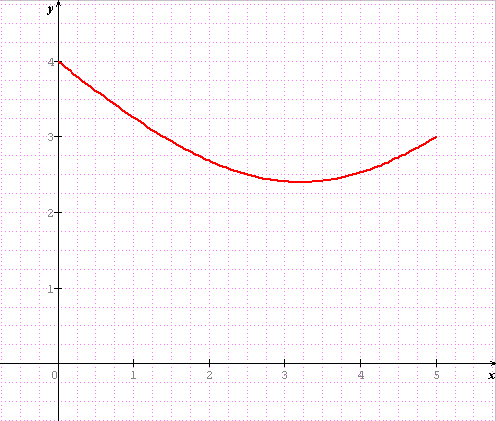
il ne te reste plus qu'à étudier y=V(25x²-160x+400)/5 qui est une branche d'hyperbole d'axe x=3 => minimum en x=16/5 qui donne y=12/5
Philoux
***edit jerome***
oups je ferme la balise [/b]
il ne te reste plus qu'à étudier y=V(25x²-160x+400)/5 qui est une branche d'hyperbole d'axe x=16/5 => minimum en x=16/5 qui donne y=12/5
Philoux
oula non il y en une qui est pas encore de mon niveau je croi 
19:09 est, sauf erreur, accessible aux 1° :
Thalès,
racines carrées
pas de trigo...
Philoux
Pour la méthode de muriel je dois calculer l'angle aBc pour trouver MH non ?
à propos de quoi, muriel ? 19:30
à part Pythagore et Thalès je ne pense pas avoir utilisé autre chose 
mais je ne suis pas familier des programmes scolaires
Philoux
j'ai cité trigo ne sachant pas sur quoi butait shikamaru
ah ok : je ne désirais pas introduire des sin et cos pour ne pas perturber shikamaru
peut-être ai-je eu tort, alors...
Bon week-end à tous !
Philoux
aprés avoir fait la mèthode de muriel je trouve que :
AM^2= (x cosB)^2 + (4-x sinB)^2
est-ce cela ????
mais la valeur de l'angle est une valeur approchée . normal ?
est-ce que sin(ABC) est une valeur approchée ?
(ce qui revient au théorème de Thaslès, je te l'accorde  )
)
je trouve que MH=3x/5
mais je bloque pour Mk 
est ce que Mk=(20-4x)/5 ??????
et donc je trouve
f^2=(25x^2-160x+400)/25
mais je n'arrive pas j'ai d'ai toute pour f
f=(5x- (160x)+20)/5
(160x)+20)/5
petite erreur
mais avant, il faut vérifier que n'est jamais négatif pour tou x dans [0;5]
comme la fonction racine est croissante, f amême variation que la fonction x
et celle ci tu peux étudier sa variation 
mon prof ma fait la remarque ce matin mème 
bon hé bien merci alors c'est gentil de m'avoir aider





