Inscription / Connexion Nouveau Sujet
Trouver une tangente à partir d'un point donné
Bonjour,
Je vais vous présenter mon sujet, cela fait plus d'un jour que je ne comprends comment résoudre cette exercice.
La fonction: 3/100x3+3/20x2
Sa dérivée: 9/100x2+3/20x
Je dois trouver le point de contact d'une tangente à la courbe sachant que la tangente passe par le point P(10;15).
Avec la formule pour trouver l'équation réduite de la tangente je me retrouve avec ça:
yp=f'(a)(xp-a)+f(a)
Donc je résous l'équation pour trouver a et je me tombe sur un polynôme du 3ème degré: 15=-6/100a3+75/100a2+3a
Que je réduis au 2ème degré: 0=-6/100a2+75/100a-18
Du coup je calcule le discriminent, celui-ci est négatif donc l'équation ne possède pas de solution et je reste bloquer dessus..
Mon résonnement je le tiens de cette vidéo: https://www.youtube.com/watch?v=2AJlmuIuYXA sauf que dans son cas le discriminent est postif du coup il a bien des solutions pour trouver a.
Je ne vois pas ou j'aurais pu faire une erreur..
Oui c'est ce que j'avais trouvé mais j'ai fait une faute de frappe en vous le réécrivant.
J'essaye et je vous recontacte
Du coup j'ai bien simplifié et remplacé et j'ai toujours le même problème je tombe sur un trinôme du 3ème degré: 0=-6/100a3+75/100a2+3a-15
Ou ce qui revient au même
Y avait-il d'autres questions avant ?
Une calculatrice formelle donne 2,7299
Bonjour,
du 3ème degré ce n'est pas un trinome...
on dit un polynome du 3ème degré
il y a des erreurs (je ne les ai pas identifiées car pas refait les calculs)
en effet il y a réellement 3 tangentes qui passent par P
comme le montre une détermination approchée avec Geogebra (en réglant à la main les curseurs pour que les tangentes passent à peu près par P)
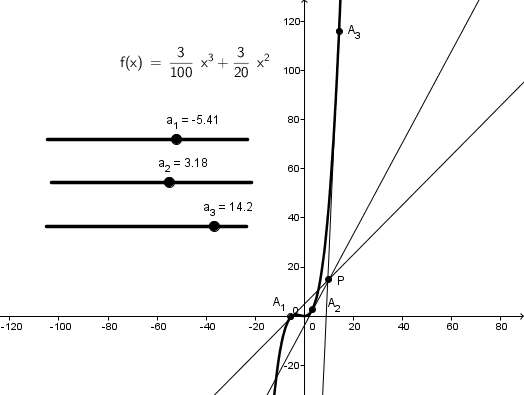
les valeurs obtenues sont à priori peu engageantes pour espérer que une résolution de l'équation de degré 3 (la bonne) en a soit autrement que par approximations
(ou alors suspecter une erreur dans l'énoncé ...)
je trouve :
... Ou ce qui revient au même

(erreur de signe sur le coefficient de x3)
la résolution formelle (au logiciel) de cette équation donne bien 3 solutions en accord avec les valeurs approchées "expérimentales" précédentes :
mais dont les valeurs exactes (avec radicaux) sont totalement inutilisables, comme d'habitude avec les équations de degré >2
salut,
on aimerait avoir des nouvelles de cet exercice ...
Je confirme.
abscisse/ordonnee/equation de la tangente
Un programme Xcas qui permet de construire ou de verifier des exercices sur ce theme.
On copie colle ce programme dans l'editeur de programmes, on l'interprete en appuyant sur OK
La fonction:
1/ renvoie les coordonnees des points de tangence et les equations reduites des tangentes
2/ ouvre une fenetre graphique affichant la courbe de la fonction, les points de tangence et les tangentes
/*****************************************************************************
**************** Tangentes à une courbe passant par un point P ***************
*****************************************************************************/
//Renvoie coordonnées des points de tangence et équations réduites des tangentes dans une liste, affiche le graphique dans DispG
TangentesCourbe(T,u,v,opt):={ //T expression, u et v coordonnées de P, opt=0 si approx et 1 si exact
local G,sol,s,k,j,L;global x;
DispG;ClrGraph;G:=plot(T,x=-20..20,affichage=epaisseur_ligne_2,xstep=0.01);//modifier -20..20 ?
legende(point(u,v),"P");
DIGITS:=4;
si opt==1 alors
sol:=resoudre(v-T=diff(T)*(u-x));//résolution exacte, evalf(ans()) donnera les approx
fsi
// si on obtient unable to isolate x in ... conjecturez les intervalles en utilisant les points d'intersection
// de la courbe bleue avec l'axe des abscisses et recommencez avec opt=0
si opt==0 alors
sol:=NULL;
plot(v-T-diff(T)*(u-x),x=-20..20,couleur=bleu,xstep=0.01);// pour mieux voir les intervalles
saisir("Séquencez des intervalles contenant \nles abscisses des points de tangence\npar exemple -3.2..0.2,2..7",L);
L:=[L];
pour k de 0 jusque size(L)-1 faire
//bisection_solver car les méthodes type newton ne donnent pas toutes les solutions
sol:=sol,moyenne(resoudre_numerique(v-T=diff(T)*(u-x),x,L[k],bisection_solver));//résolution approchée
fpour
sol:=[sol];
//sol:=resoudre_numerique(v-T=T'*(u-x));//résolution approchée
//sol:=set[op(sol)]; // pour racines multiples
fsi
s:=size(sol);
si s==0 alors
afficher("Il n'est pas possible de construire une droite passant par P et tangente à la courbe");
retourne []
fsi
si s==1 alors
afficher("Une seule droite passant par P est tangente à la courbe");
point(sol[0],simplifier(subst(T,x=sol[0])),affichage=epaisseur_point_3);
retourne [sol[0],simplifier(subst(T,x=sol[0])),equation(tangente(G,sol[0],couleur=rouge))]
fsi
afficher(s+" droites passent par P et sont tangentes à la courbe");
seq(point([sol[j],simplifier(subst(T,x=sol[j]))],affichage=epaisseur_point_3),j,0,s-1);
retourne seq([sol[j],simplifier(subst(T,x=sol[j])),equation(tangente(G,sol[j],couleur=rouge))],j,0,s-1);
}
:;


