Inscription / Connexion Nouveau Sujet
Un cube tromqué
Bonjour à tous j'ai un dm pour jeudi et je suis bloqué à cette exercice ça serai gentil de maidé merci bocou davance
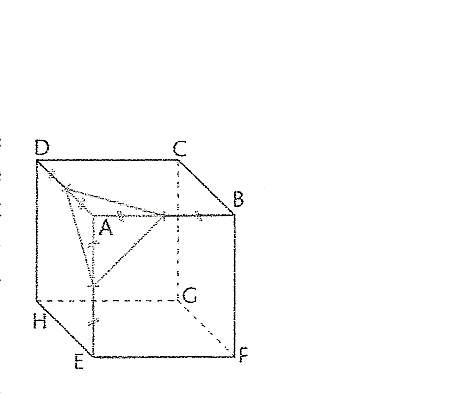
Sujet: ABCDEFh est un cube d'arrete 3 cm. on lui enleve le tatrraedre de sommet A et dont la base est la section du cube par le plan passant par les milieux de trois arrete issues de A
question 1 a) construire une figure et racer , en rouge, le solide S obtenu apré les differentes troncatures
b) decrire S nombre et nature des face, nombre de sommet, nombre d'arrete
justifier la reponse concernan la nature des face
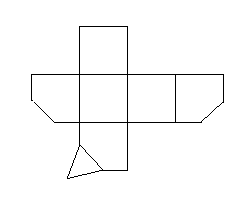
question 2 a) dessiner un patron S
b)calculer laire totale Ade ce patron
question 3 calculer le volume V de S
Un peu de tout parce que cette année en math mon point faible c'est surout la geometrie dans l'espace méla la difficulté et la question 1
le cube a 6 faces. Avec cette troncature, on lui en rajoute 1.
le cube a 8 sommets. Avec cette troncature, on lui en retire 1, et on lui en rajoute 3.
le cube a 12 arêtes. Avec cette troncature, on lui en rajoute 3.
...
Comme quoi, le langage a ses conventions qu'il vaut mieux
respecter si on veut avoir une chance d'être compris !
...
2b)
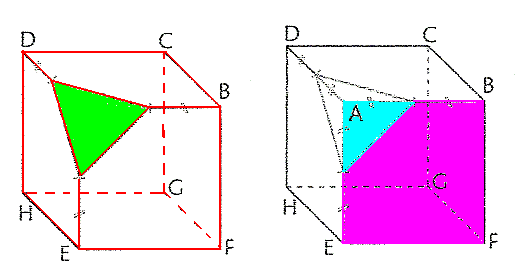
Aire du triangle bleu clair = (1/2) * 1,5 * 1,5 = 1,125 cm²
--> aire en mauve = aire d'une face du cube - aire en bleu clair
Aire en mauve = 3² - 1,125 = 7,875 cm².
---
Il y a 3 faces de même aire que la face en mauve et 3 faces de même aire que les faces du cube + la face en vert.
Aire de la figure tronquée = 3 * 7,875 + 3 * 3² + aire de la face en en vert
Fais un effort pour trouver l'aire en vert pour terminer...
-----
3)
Volume du tétraèdre enlevé = (3/2)³/6 = 27/48 cm³ = 9/16 cm³
Volume de la figure tronquée = 3³ - (9/16) = 423/16 cm³
-----
Sauf distraction. 
Merci beaucoup J-P pour l'air en vert , je peux dire que c'est trois fois l'air du triangle rectangle bleu?? donc 3*1,125=3,375cm²
Non, l'aire en vert n'est pas ce que tu dis.
Le triangle vert est un triangle équilatéral de coté = (3/2)*V2; soit un coté de 3/V2 cm (V pour racine carrée).
On peut calculer le coté du triangle vert par Pythagore (voir sur ce dessin)
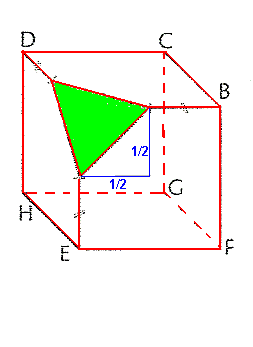
Quelle est l'aire d'un triangle équilatéral de coté = (3/V2) cm ?

Et tu n'as toujours pas compris qu'ici il faut oublier les abréviations que tu as l'habitude d'utiliser ailleurs ! Il faut écrire en français, pour le savoir, il faut lire la FAQ = Foire Aux Questions ici : 
![]() [lien]
[lien]
ainsi que le message qui est en tête de toutes les liste des messages et qui a pour titre ""A LIRE AVANT de poster, merci""
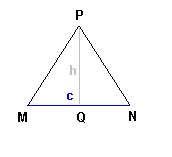
Soit un triangle MNP équilatéral de coté c
Q est le pied de la hauteur issue de P
PQ est aussi la médiatrice de [MN] --> QN = a/2
Pythagore dans le triangle PQN:
PQ² + QN² = PN²
h² + (a/2)² = a²
h² = a² - (a²/4) = 3a²/4
h = (a/2)*V3
---
Aire du triangle MNP = (1/2) * MN * h
Aire du triangle MNP = (1/2) * a * (a/2)*V3
Aire du triangle MNP = (a²/4)*V3
---
Dans le triangle vert, le coté est (3/V2) -->
Aire du triangle vert = ((3/V2)²/4)*V3 = (9/8)*V3 cm²
-----
Sauf distraction. 
Et tu n'as toujours pas compris qu'ici il faut oublier les abréviations que tu as l'habitude d'utiliser ailleurs ! Il faut écrire en français, pour le savoir, il faut lire la FAQ = Foire Aux Questions
ainsi que le message qui est en tête de toutes les liste des messages et qui a pour titre ""A LIRE AVANT de poster, merci""
En faite j'ai compris la méthode de J-P mais je ne voispas comment il a trouvé la hauteur du triangle vert
Dans la réponse du 29/03/2008 à 18:46, avec Pythagore du peux bien calculer les côtés du triangle vert équilatéral.
Et avec la connaissance de la longueur des côtés du triangle vert tu peux tout aussi trouver la longueur des hauteurs du triangle vert (avec Pythagore à nouveau)
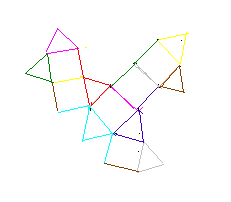
re bonjour enfaite j'ai fait lep patron de la figure mé je ne c'est pas ou placé les triangle vous pouvais m'aidez s'il vous plaît
je me suis trompé sur l'énoncé j'ai oublié de preciser dans l'enoncé qu'on procédé à l'peration analogue à partir des sept autres sommets donc si vous pouvez m'aider encore uen fois si ça vous derange pas pour la question 2 et 3
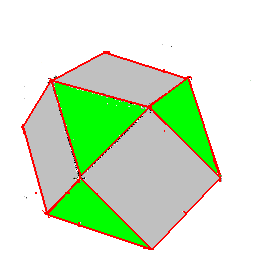
Il y a 8 triangles verts (1 par sommet du cube entier).
Il y a 6 carrés gris (1 par face du cube entier)
On a trouvé que le coté d'un triangle vert était égal à : (3/2)*V2
C'est aussi la mesure d'un coté des carrés gris.
Aire d'un carré gris : [(3/2)*V2]² = 4,5 cm²
---
On a déjà montré que l'aire d'un triangle vert = (9/8)*V3 cm²
---
Aire totale du cube tronqué : 8 * (9/8)*V3 + 6 * 4,5 = 27 + 9V3 cm²
-----
Volume cube tronqué = 3³ - 8 * (9/16) = 27 - 4,5 = 22,5 cm³
-----
Sauf distraction, vérifie.