Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Angles orientésTopics traitant de angles orientés [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Un exercice sur les angles orientes : vrai ou faux

Posté par
guildwars 03-01-08 à 00:50

Voila, J'ai un exercice sur les angles orientes, c'est un Vrai ou Faux, mais le probleme c'est que je ne sais pas comment expliquer les reponses.

Voici l'enonce :

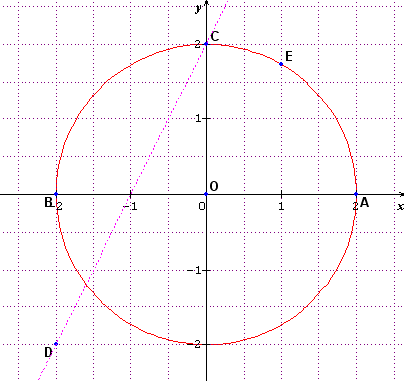
Dans un repere orthonormal direct (O;i,j), on donne les point A(2;0), B(-2;0), C(0;2). D(-2;2) et E(1;\sqrt{3})
a) Le triangle OEA est equilateral.
b) (\vec{OE};\vec{DC})=\frac{\pi}{3}
c) (\vec{AE};\vec{OD})=-\frac{\pi}{9}

Je sais pas si elles sont vraies ou fausses, car sur le dessin c'est tres proche et je ne sais pas comment expliquer, donc j'ai vraiement besoin de votre aide!

Merci d'avance.

Posté par
patrice rabillerre : Un exercice sur les angles orientes : vrai ou faux 03-01-08 à 04:30

Bonjour,
Si tu as vu les coordonnées polaires alors :
A a pour coordonnées polaires (2;0)
B a pour coordonnées polaires (2;)
C a pour coordonnées polaires (2;/2)
D a pour coordonnées polaires (2\sqrt 2;-3/4)
E a pour coordonnées polaires (2;/3).
On en déduit que :

a) Le triangle OEA est bien équilatéral car OA=OE=2 et \(\vec{OA};\vec{OE}\)=\frac{\pi}{3}

b) La droite (DC) a un coefficient directeur égal à 2 donc l'angle \(\vec{OA};\vec{DC}\) a une tangente égale à 2.
Donc \(\vec{OE};\vec{DC}\)=\(\vec{OE};\vec{OA}\)+\(\vec{OA};\vec{DC}\)=-\frac{\pi}{3}+\arctan 2\neq\frac{\pi}{3}.

c) \(\vec{AE};\vec{OD}\)=\(\vec{AE};\vec{OA}\)+\(\vec{OA};\vec{OD}\)=\frac{-2\pi}{3}-\frac{3\pi}{4}=\frac{5\pi}{12} (mod 2)

Un exercice sur les angles orientes : vrai ou faux

Posté par
guildwarsre : Un exercice sur les angles orientes : vrai ou faux 03-01-08 à 10:19

Merci c'est tres bien explique, mais le point D est (-2;2) et vous avez fait avec (-2;-2)

Posté par
guildwarsre : Un exercice sur les angles orientes : vrai ou faux 03-01-08 à 11:10

Ca va tout changer pour la 2) et la 3)?

Posté par
patrice rabillerre : Un exercice sur les angles orientes : vrai ou faux 03-01-08 à 20:02

Désolé, j'ai mal lu l'énoncé

Oui, ça change tout : le coefficient directeur de la droite (CD) devient -2 au lieu de 2 et l'angle \(\vec{OA},\vec{OD}\) ne vaut pas \frac{-3\pi}{4} mais \frac{-\pi}{4} Heureusement que j'avais joint le dessin pour que tu puisses vérifier


Rechercher
Menu
Espace membre
4 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1726 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !