Bonsoir,
f(x) n'est pas claire

ohh ! je m'excuse. je repète : f(x)= 2√x -x . J'ai vraiment besoin de l'aide svp

attention je trouve f(1) = 1 !!!!!!!!
21 - 1 = 2-1 =  1

en effet c'est un quart de cercle puique x>0 et y>0 en effet x > x pour x[0;1] ddonc 2x>x donc y>0

pardon, ce n'est pas 1/4 de cercle car: on n'a pas une eqution de la forme (y-y_centre)²+(x-x_centre)²=rayon²

Bonsoir,

la fonction y = ((x(x-2)) sur x [0;1] est bien un quart de cercle.

Conclusion : ça ne se voit pas directement à la tête de l'équation ...

Il faut "supprimer les radicaux" :
y + x = 2x

on élève au carré et on obtient effectivement alors quelque chose qu'on peut "comparer" avec l'équation d'un cercle,
où d'un bout de cercle si on se restreint sur x [0;1] et y 0.

On obtient en fait l'équation d'une parabole, d'axe de pente -1 (à 45°)
mais on ne le demande pas (ouf !), juste que ce n'est pas un cercle
C'est à dire que l'existence de termes en xy interdit une équation de la forme (x-a)² + (y-b)² = R²

la courbe complète, avec en vert le cercle supposé :

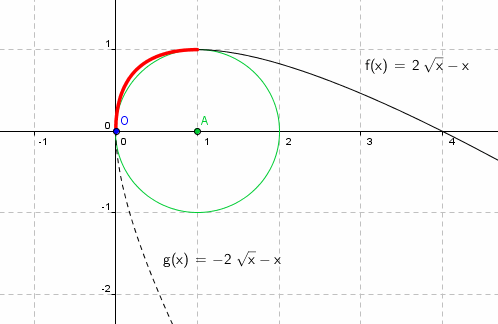
On peut aussi raisonner ainsi :
conjecturons un quart de cercle, celui-ci étant tangent en O à l'axe des ordonnées et la tangente en (1; 1) horizontale, son centre est donc A(1; 1)
Il suffit de prendre le point x = 1/2, qui si c'était un cercle donnerait y = (3)/2 pour se convaincre que cette conjecture est fausse.

évidemment cela ne prouve rien, à moins de prouver que les tangentes sont comme on le voit. Et le calcul de ces tangentes est aussi compliqué que l'élévation au carré précédentes

Mais aussi la courbe peut être simplement "étendue" sur tout R⁺
et alors x = 4 donne déja quelque chose d'éloigné d'un cercle.
Et même pire la limite quand x ...