Inscription / Connexion Nouveau Sujet
Une suite de carrés / Suite géométrique
Bonjour, je viens poster sur le forum car je suis actuellement bloqué dans un dm qui est a rendre pour demain.
A0B0C0D0 est un carré de côté 1.
On place sur ses côtés les points A1B1C1D1 tels que A0A1= 1/4 A0B0, B0B1= 1/4 B0C0, C0C1= 1/4 C0D0 et D0D1 = 1/4 D0A0 puis on itére la construction pour former une suite de carrés AnBnCnDn
2. Quelles conjectures peut-ont faire sur les aires des carrés ainsi construits ? sur leurs côtés ?
Les aires des carrés vont constamment réduire jusqu'à tendre vers une certaine limite qu'on déduira par la suite. Les côtés eux vont aussi constamment réduire. (Cela me parait un peu léger mais je ne me suis pas attardé sur cette question en décidant d'abordé en premier temps les calculs)
3. Soit Cn le côté du carré AnBnCnDn.
a. Démontrer que pour tout n > 0, Cn+1 = ((Racine carré 10)/4)*Cn
Alors la j'ai fais Pythagore vite fait et j'ai démontrer
b. En déduire Cn en fonction de n
Suite géométrique donc Cn = ((racine carré 10)/4)^n
Je bloque a partir de la:
c. A partir de quelle étape aura-t-on Cn > 0.001 ? (J'ai penser quand Cn tend vers + infini)
4. On considére la ligne brisée A0A1A2A3...An et on nomme Ln sa longueur pour n > 1
a. Démontrer que pour tout n > 1, Ln = 1/4 * 1-((racine carré 10)/4)^n / 1-((Racine carré 10)/4)
b. Conjecturer la limité éventuelle de la suite (Ln)
Je vous ais joint un scan de la figure
Ps: Je suis désolé je suis tout nouveau sur ce site et je n'ai pas encore trouvé l'endroit pour pouvoir écrire avec une syntaxe correcte les formules
Bonjour,
Les aires des carrés vont constamment réduire jusqu'à tendre vers une certaine limite qu'on déduira par la suite. Les côtés eux vont aussi constamment réduire.
extraordinaire, un carré de côté nul qui a une aire non nulle !

la limite dont on parle ensuite n'est pas la limite de l'aire, mais d'un autre "truc" : une ligne brisée qui cumule des morceaux de côtés !
Le reste du début me semble cohérent (pas vérifié les valeurs exactes)
A partir de quelle étape aura-t-on Cn > 0.001 ? (J'ai penser quand Cn tend vers + infini)
on aura Cn > 0.001 dès le début puisque C0 = 1
il s'agit sans doute de : A partir de quelle étape aura-t-on Cn
et la réponse doit être : dès que n > une valeur précise qu'on te demande de déterminer.
la 4 : tu as déja calculé les côtés Cn
les segments de ta ligne brisée sont les quarts de ces côtés !
donc il s'agit de calculer la somme des Cn/4 :
C0/4 + C1/4 + ... + Cn/4
et comme la suite Cn est une suite géométrique, Cn/4 aussi bien sûr (même raison mais premier terme 1/4 au lieu de 1), la somme des termes de cette suite c'est question de cours.
Bonjour,
J'ai le même exercice que toi en DM pour la rentrée. Je voudrais savoir comment tu as utilisé Pythagor s'il te plait
Bonjour,
tu n'as pas cherché à réfléchir assez !
la 4 : tu as déja calculé les côtés Cn
les segments de ta ligne brisée sont les quarts de ces côtés !
donc il s'agit de calculer la somme des Cn/4 :
C0/4 + C1/4 + ... + Cn/4
et comme la suite Cn est une suite géométrique, Cn/4 aussi bien sûr (même raison mais premier terme 1/4 au lieu de 1), la somme des termes de cette suite c'est question de cours.
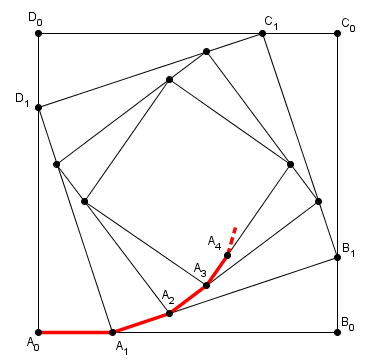
on demande la longueur de la ligne brisée rouge A0A1A2A3A4...An
Merci je comprend mieux et comment on fait pour b. Conjecturer la limité éventuelle de la suite (Ln)
la 4b découle directement de la 4a et de
donc
(il suffit en fait de savoir ce qu'est une limite et les règles élémentaires de calcul sur les limites pour non seulement conjecturer mais le prouver)
Bonjour,
J'ai un problème un peu similaire à celui-ci mais je ne comprends pas comment vous avez démontré cn+1 en fonction de cn.
J'ai compris qu'il fallait utiliser Pythagore mais je suis bloqué.
Merci d'avance pour votre aide.
Le côté du plus petit carré :
(cn+1)2 = (1/4cn)2 + (3/4cn)2
Je pars de là mais ensuite je ne vois pas ce que je peux faire.
Bonjour,
"un peu similaire"
donc ce n'est pas exactement le même, quelle différence y a-t-il entre les deux énoncés ?
les mêmes carrés ou pas ? sinon il fallait créer ta propre discussion sur cet exo différent
juste des questions légèrement différentes ? lesquelles ?
si c'est juste ça, OK restons ici
(cn+1)2 = (1/4cn)2 + (3/4cn)2 = ((1/4)² + (3/4)²)(cn)² = ...
(edit : oubli de l'exposant)
Ah oui, j'oublie souvent.
Du coup j'obtiens
(cn+1)2 = 5/8 x cn2
Mais je ne comprends pas, c'est différent de 10/4 qui est indiqué dans l'énoncé de départ.
dans le cas présent il vaut effectivement mieux de pas simplifier 10/16 car 16 étant un carré = 4², il va "sortir" du radical en extrayant la racine
et puis , pas
Ah oui d'accord !
Merci beaucoup.
Je regarde la suite et je vous proposerai ma solution si vous voulez bien.
Merci
- On me demande de préciser la nature de la suite (cn)
J'ai indiqué qu'elle se présentait sous la forme
cn+1 = ( 10)/4 x cn
10)/4 x cn
cn+1 = q x cn
Cn est donc une suite géométrique de raion q=( 10) /4 et de premier terme co = 1
10) /4 et de premier terme co = 1
- On me demande ensuite de déduire cn en fonction de n
J'ai utilisé la formule
cn = c0 x qn
J'obtiens
cn = (( 10)/4)n
10)/4)n
-On me demande ensuite de déterminer à partir de quelle étape n on aura cn < 0,001
Là je bloque.
J'ai essayé en écrivant
(( 10)/4)n = 0,001
10)/4)n = 0,001
mais je ne trouve pas.
Pourriez-vous m'aider ?
La dernière question concerne la longueur de la ligne brisée A0, A1, A2...An
J'ai utilisé la formule
Premier terme *( (1-qnombre de termes)/1-q)
J'obtiens
1/4 * (1-( 10)/4)n) / 1-(
10)/4)n) / 1-( 10)/4
10)/4
Est-ce exact ?
Je vous remercie par avance
à partir de quelle étape n on aura cn < 0,001
à ce niveau (1ère) on ne connait pas les logarithmes
donc deux façons de procéder : la calculette ou le tableur pour
- soit calculer un par un les Cn
- ou jouer au "trop grand ou trop petit"
essayer n = 10, C10 est il plus grand ou pus petit que 0.001 ?
si c'est trop grand essayer un n plus grand pour diminuer Cn
sinon essayer un n inférieur
Premier terme *( (1-qnombre de termes)/1-q)
parenthèses mal placées :
Premier terme * (1-qnombre de termes)/(1-q)
idem pour le calcul numérique avec en plus des parenthèses non appariées.
je suppose que tu as écris correctement avec les barres de fractions sur feuille.