salut!!
alors pour le premier exercice,
quel que soit x réel, x²+2 est toujours positif et s'annule jamais. donc le signe de la fraction dépend uniquement du signe du numérateur x², qui ne s'annule que pour x=0.

mais ce n'est pas la réponse à la question. pour établir le tableau de variations de f, il te faut étudier le signe de f'. et ce n'est pas exactement ce que tu fais

Merci de m'aider Nisha.
Mais je ne comprend pas pourquoi il faut étudier le signe de f'(x). Pourquoi étudier f(x) ne suffit pas ? Si je fait le tableur de variation ce devrait marcher non ?

salut!
tu peux étudier f(x)
dans ce cas, je crois que ta fonction est paire (évident à montrer) , positive quel que soit x, et elle s'annule en 0.
donc ta fonction est décroissante sur ]-;0] et croissante sur [0;+[

ps: j'ai un petit souci, à la question 1.B) tu ne te serais pas trompée sur le signe de l'inégalité (au lieu de ) car d'après la question 1.A cette expression est positive et nulle pour x=0.

exercice 2:

a= 0,459 621 126
b= 0,459 621 127
a<b donc

tu utilises juste , l'expression developpée
tu mets A et B sous cette forme.
et au lieu de faire la différence, tu fais le quotient! ensuite tu vas comparer les expressions terme à terme.
tu auras donc
tu compares à 1, et tu compares à 1.

Ha oui pardon je me suis trompée dans les signes :

B°)Justifier alors que pour tout réel x, f(x) - 0

2. Démontrer de façon analogue que pour tout réel x, f(x) 1 et conclure.

En tout cas, merci beaucoup de me consacrer de ton temps pou m'aider, c'est très gentil.

-----------
EXERCICE N°1

Donc si j'ai bien compris pour l'exercice N°1 il faut faire :

1°) A : f(x)-

    B: Toujours positif
       Donc le signe de dépend de

Je fais le tableau de variation :

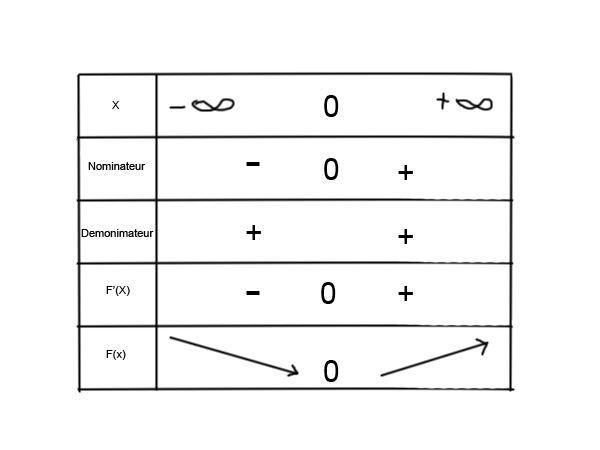
*** image placée sur l'***

Mais je comprend pas, j'ai une courbe décroissante, je vois pas où est mon erreur.

2°) f(x)-1

Donc, le quotient s'annule si
0
=-2
Impossible alors toujours positif.
On en déduit que le signe de dépend de

Mais est toujours positif aussi donc je ne comprend pas non plus, pourtant je ne crois pas que mon opération soit mauvaise.

-----------
EXERCICE N°2

Il faut donc écrire : 0,459 621 126+ et 0,459 621 127+


Je fait le quotient (Mais pourquoi ?)


Je ne suis pas certaine de la prochaine étape :

Ensuite, je n'ai pas bien compris ce que te veux dire par "comparer les expressions terme à terme."

Savoir qui est le plus grand entre et ?

salut!
exercice 1.
1-B) ta réponse est juste, si tu relis bien ce que j'ai marqué, ta courbe est décroissante sur ]-infini;0] et croissante sur [0;+infini[. ce qui correspond à ton tableau de variations

2.
x^2+2 étant

x^2+1 étant positif, f(x)-1 est du signe du numérateur, c'est-à-dire négatif
f(x)-1<0 donc f(x)<1
et en réunissant les deux inégalités (Q-1. et Q-2.), tu montres ce qu'il fallait démontrer.
1/2<f(x)<1

exercice 2:
je t'ai dit, quand tu developpes X+(1/X), tu trouves (X²+1)/X
donc,



pour voir lequel des deux est le plus grand, tu fais le quotient et tu compares le quotient à 1.
si A/B < 1 alors A < B
si A/B > 1 alors A > B

donc tu auras:



et après tu compares chaque fraction à 1

Je suis vraiment désolée, mais je ne comprend pas ce que vous voulez dire par ces opérations :



Le quotient, c'est bien le résultat d'une division ?
Donc si oui, A/B ca serait plutot :

Divisé par


et donc

Multilié par


Donc



Mais en suite, je ne vois pas comment avancer a part en simplifiant mais je suis pas certaine que ce soit bon :



donc



Donc A à B
Donc A = 0,459 621 126+ B = 0,459 621 127+

C'est bien ça ?

le résultat de A/B, tu arrives exactement à ce que j'avais écrit.
donc ensuite pour comparer, c'est tès simple.

1_: 0,459 621 126 < 0,459 621 127
  (0,459 621 126)²< (0,459 621 127)²
  (0,459 621 126)²+1 < (0,459 621 127)²+1
  [(0,459 621 126)²+1)]/ [(0,459 621 127)²+1] < 1


2_ 0,459 621 127 >  0,459 621 126
   (0,459 621 127)/(0,459 621 126) > 1

tu as donc le produit de deux termes, le premier < 1 et le deuxième > 1.
en multipliant les deux, tu obtiens un résultat > 1.
soit A/B > 1
donc A > B

après tu peux vérifier à la calculatrice pour etre sure.

Ha ok, c'est bon j'ai compris maintenant !
Merci beaucoup pour ton aide, je crois que je n'aurais jamais réussit toute seule.
C'est vraiment super sympa d'aider ainsi les élèves.

Excuse moi, j'ai un dernier soucis, ont a dit dans l'exercice N°1 que la fonction N°1 est décroissante sur ]-l'infinie;0] et croissante sur [0;+l'infinie[
Et pourtant dans la question, il faut montrer que pour tous réel x, le fonction est supérieur ou égale à 0.
Si a un moment elle est décroissante, elle ne peut pas etre toujours supérieure ou égale à 0.
C'est ça que je ne comprend pas très bien.

Ha nan je crois avoir troué, un carré est toujours positif donc mon tableau est faux !
La fonction est toujours croissante sur IR ! C'est bien ça ?

non, le tableau est correct. décroissante ne signifie pas qu'elle est négative.
si tu prends la courbe de f(x)=x², c'est pratiquement le même cas que ta fonction. elle est décroissante sur ]-infini;0] , mais elle reste positive.
c'est pareil pour f(x)=|x| .
ta fonction est toujours positive, et positive ne signifie pas croissante.
de toute façon, les flèches te donnent à peu près l'image de la figure.

ps: je crois qu'on a fait une erreur dans le tableau, au lieu de mettre 0, tu dois mettre 1/2.
parce que là en fait, on étudies les variations de f(x)-1/2 (qui est positive) et non f(x) (qui est supérieure ou égale à 1/2).