Inscription / Connexion Nouveau Sujet
valeur absolue
Bonjour,
Je voudrais savoir pourquoi la fonction valeur absolue n'est pas dérivable en je voudrais savoir quelle est la dérivée de cette fonction?
salut
f(x)=|x| n'est pas dérivable en 0
mais pour x> 0 f(x)=x => f'(x)=1
pour x< 0 f(x)=-x => f'(x)=-1
la dérivée est la pente de la tangente au point M(x,f(x)),
essaie de tracer la pente en 0 de f(x)=|x|
Oui je sais, la dérivée en un point est le coefficient directeur de la tangente en ce point, si la tangent est verticale je comprend, le coefficient directeur est infini, donc la dérivée n'existe pas, par exemple pour f(x)=
x, en 0, or ici elle est horizontalen le coefficient directeur est donc 0, donc je dirais que f'(0)=0.
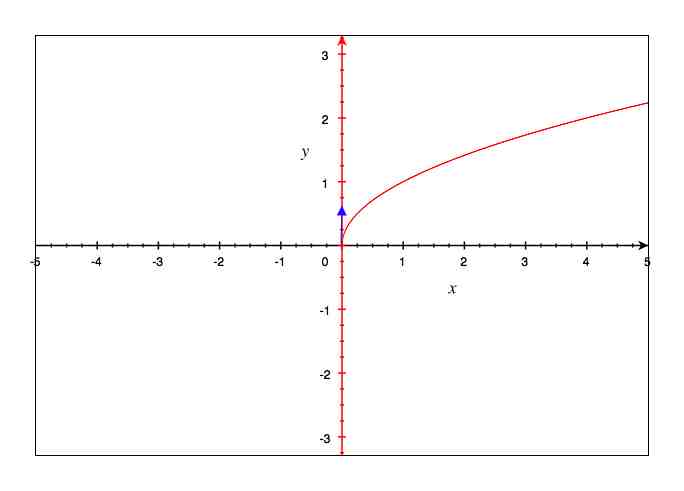
non pour la fonction racine
la dérivée est
quand x tend vers 0+ f'(x) tend vers +oo, la demi-tangente est verticale en 0
Oui, mais en 0, une tangente verticale? ce n'est pas possible, fonction racine carrée est dérivable sur R-{0}? Sinon par exemple pour la fonction carrée, en 0 il y a aussi une tangente horizontale donc elle n'est pas dérivable en 0?
en fait c'est une demi tangente, car racine n'existe pas pour x<0
pour les x> 0, l'équation de cette tangente tend vers x=0 lorsque x->0
ici le coefficient directeur n'est pas calculable ..
mais par "prolongation" on peut dire qu'il est égale à +oo,
mais on le voit mieux sur un dessin ou voir mon post de 22:12 pour le calcul de la limite de f'(x) en 0+..
Merci. je suis embetant mais j'essaye vraiment de comprendre les dérivées graphiquement, et donc pour un tangente horizontale, le coefficient directeur est 0, c'est le cas de valeur absolue, alors pourquoi la dérivée de valeur absolue de x en 0 n'est pas 0?
non à gauche pour x<0 f'(x)=-1
non à gauche pour x>0 f'(x)=-1
mais en 0 comment peut-on tracer une tangente ?
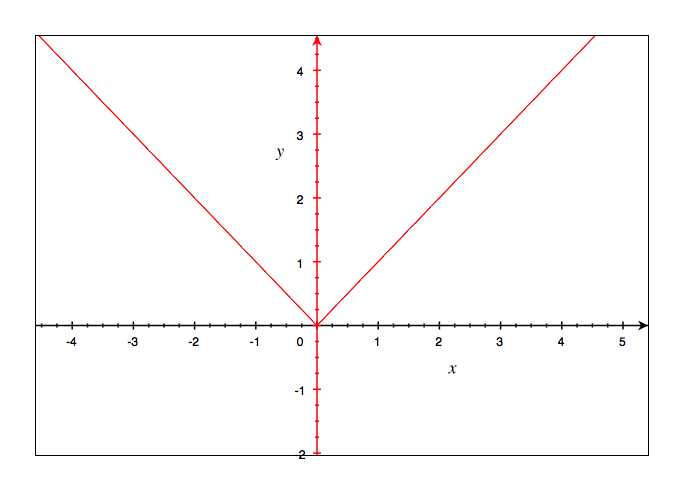
en fait en 0, c'est pointu, les tangentes ne sont possibles que quand la courbe est lisse ou douce, dans les zones de fort changement (pointe, changement brusque d'orientation décroissante puis croissante sans jamais être nul ..), le calcul de dérivée n'est pas possible..
ahhh oui je vois c'est une tangent verticale, j'aurais dis une tangente horizontale d'équation y=0 donc la faconction valeur absolue de x est définie sur R-{0}?
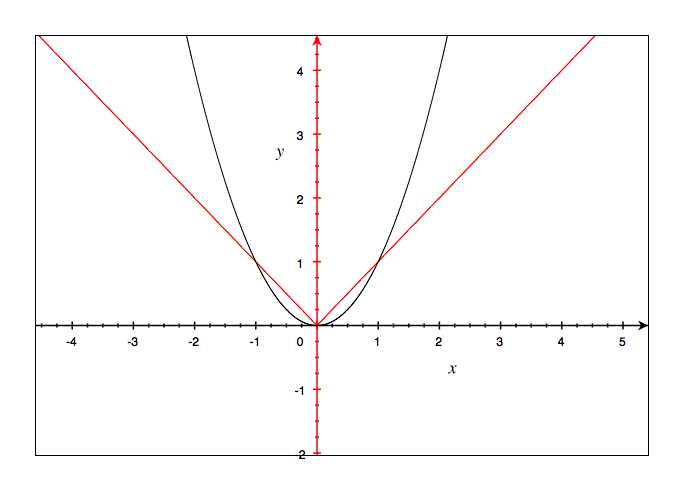
la parabole ( en noir) a une tangente y=0 , tu vois que le sommet de la parabole épouse la droite y=0 (on a l'impression qu'il y a plusieurs points de contact avec y=0) par contre on voit clairement que la fonction valeur absolue (en rouge) a qu'un seul point de contact avec y=0..
Annuler
connectez vous