Inscription / Connexion Nouveau Sujet
Valeur absolue
Bonjour pouvez me corriger cet exercice et m'aider pour la question 3).
S'il vous plait merci d'avance.
exercice:
La fonction f définie sur R par : f(x)=|-x + 1| - |2x - 1|
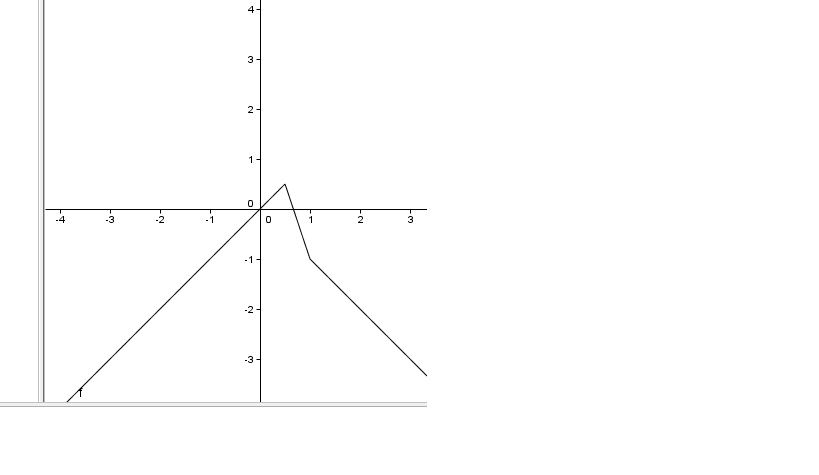
Cf sa courbe représentative dans un repère orthonormé.
1)Exprimer f(x) sans utiliser les barres de valeur absolue suivant les valeurs de x dans R
== Je trouves :
|-x + 1|= -x+1 si x 1
et x-1 si x 1
|2x+1| = 2x-1 si x 1\2
et -2x+1 si x 1\2
2)Dresser le tableau de variation de f
si x 1 f(x)= 3x-2
si 1 x
1\2 f(x)=x
si x 1\2 f(x)= -3x+2
voici mon tableau :
x - 1\2 1
1
f(x)
-1\2
j'espère que vous avez compris. MAIS JE N'ARRIVE PAS A TRACER LA COURBE Cf pouvez m'aider s'il vous plait .
si f(x)=(1-x)-(1-2x)=x
si f(x)=(1-x)-(2x-1)=-3x+2
sif(x)=(x-1)-(2x-1)=-x
sa courbe est en trois parties: demi droite, segmnt demidroite
Bonjour,
On y va étape par étape pour éviter les erreurs de calculs ^^
|-x+1| = |1-x| = 1-x, si (1-x) 0 donc si 1
0 donc si 1 x
x
x-1, si (1-x) 0 donc si 1
0 donc si 1 x
x
|2x-1| = 2x-1, si 2x-1 0
0  2x
2x 1
1  x
x 1/2
1/2
1-2x, si 2x-1 0
0  2x
2x 1
1  x
x 1/2
1/2
Donc
si x 1, f(x) = x-1-(2x-1) = -x
1, f(x) = x-1-(2x-1) = -x
si 1/2 x
x 1, f(x) = 1-x-(2x-1) = 2-3x
1, f(x) = 1-x-(2x-1) = 2-3x
si x 1/2, f(x) = 1-x-(1-2x)= x
1/2, f(x) = 1-x-(1-2x)= x
Sauf distraction de ma part 
OK MERCI maintenant je vais essayer de comprendre tous cala
et encore merci a sloreviv et Asap
pouvez m'accorder du temps pour essayer de comprendre tous cela.
c'est bon j'ai compris mais je suis bloqué sur la réalisation du tableau de variation pouvez m'aider sloreviv ou Asap
eh bien il est comme la courbe :
x | 0.5 1
---------------------------------------------------------------------------------------------------
f(x) |