Inscription / Connexion Nouveau Sujet
Valeur minimale d'une distance en fonction d'un point
Bonjour, j'ai un dm de maths pour la rentrée mais je ne sais pas comment trouver la réponse à une question.
Je vous donne l'énoncé ainsi que mes recherches :
On considère la courbe C d'équation y = racine carrée de x dans un repère orthonormé (0;vecteur i; vecteur j).
On note M(x; racine carrée de x) un p point de C et on considère le point A(2;0).
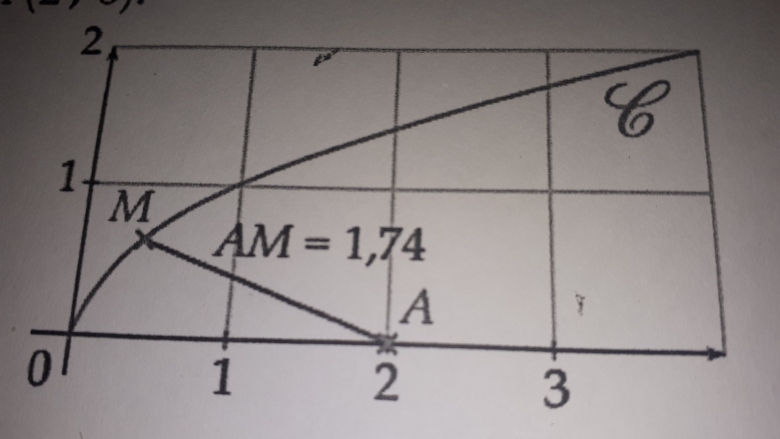
1)vérifier que AM= racine carrée de (x2 -3x +4).
2) déterminer la position de M telle que AM soit minimale.
1) alors j'ai utilisé une formule et j'ai vérifié la distance AM.
2) et c'est là que je ne sais pas comment faire pour trouver la valeur minimale, si quelqu'un pourrait m'aider svp... merci d'avance.
bonsoir
alors méthode "brutale" si tu sais dériver une racine carrée, étude de fonction...(non nécessairement la plus futée)
ou bien
se dire que la distance est minimale, lorsque le carré de cette distance est minimal
et utiliser le programme de seconde (parabole, etc) pour déterminer le minimum...
à toi....en fonction de ton programme....et de tes savoirs...
Bonjour,
Tu as accès à des symboles avec la touche  sous la zone de saisie.
sous la zone de saisie.
Pour 2) , tu peux commencer par écrire x2 -3x +4 sous forme canonique.
Tu pourras en déduire le minimum de x2 -3x +4 .
Merci !
J'ai trouvé pour minimum S( 3/2 ; 7/4 )
Ça veut donc dire que si M à ces coordonnées, AM sera minimale ?
ce point ne me semble pas sur ta courbe....
réfléchis pour reformuler ta réponse....mais tu n'en es pas loin
Non, ce point n'est pas sur la courbe...
Tu as trouvé que le minimum de x2 -3x +4 est 7/4 quand x = 3/2 .
Pour x = 3/2 on a x2 -3x +4 = 7/4 .
Or AM =  (x2 -3x +4) .
(x2 -3x +4) .
A toi de continuer.
Mais quand je remplace x par 3/2, je trouve que AM vaut environ 1,32, or ce n'est pas la bonne réponse donc je ne vois pas comment faire.. aidez moi encore un peu svp
bonjour,
la question est : "quelle est la position de M"
pas "quelle est la valeur minimale de AM"
donc "la réponse" (du bouquin, du corrigé etc) se réfère à cette position de M, pas à la valeur de AM !!
Bonsoir, étant donné que les coordonnées de M sont (x; x) alors avec les coordonnées du minimum on a M(3/2;
x) alors avec les coordonnées du minimum on a M(3/2; 7/4).
7/4).
En vérifiant avec geogebra, on remarque que ce point n'est pas sur la courbe...
Où est mon erreur ?
le minimum dont tu parles est sur ta parabole d'équation y=x² -3x +4 !
ne perds pas le fil de ce que tu démontres !
Tu confonds coordonnée du point sur la courbe C avec les coordonnées du sommet d'une parabole.
La parabole P d'équation y = x2 -3x +4 a pour sommet S(3/2, 7/4).
Cette parabole n'a pas grand chose à voir avec l'exercice.
Ici, tu as une fonction g(x) = x2 -3x +4 dont le minimum est 7/4 atteint pour x = 3/2 .
AM =  g(x) ; donc le minimum de AM est
g(x) ; donc le minimum de AM est  (7/4).
(7/4).
Ce minimum est obtenu pour x = 3/2 .
Pour x = 3/2 , le point M qui est sur la courbe C , a pour ordonnée  (3/2) .
(3/2) .
Pour x = 3/2 , la distance AM est égale à  (7/4) .
(7/4) .
Je répète : Regarde la chouette animation de malou.
On y voit la distance AM et les valeurs de x (en haut, c'est a ).
x n'est pas à la fois 3/2 et 7/4 !!
comment imagines tu que dans (x; √x) tu remplacerais un des x par 3/2 et l'autre par 7/4 ???
faut pas confondre
- la valeur de x pour laquelle la fonction distance(x) est minimale
- la valeur de cette distance minimale
- l'ordonnée du point d'abscisse x de la courbe C
Je pense avoir compris et trouvé la réponse !
La longueur minimale de AM est  7/4 lorsque x = 3/2
7/4 lorsque x = 3/2
Donc quand M(3/2 ;  3/2), la longueur AM est minimale !
3/2), la longueur AM est minimale !
Ai-je juste ?
oui
à condition d'écrire ici (on ne sait pas la longueur de la barre du radical ni des fractions !!)
 (3/2) parenthèses obligatoires.
(3/2) parenthèses obligatoires.
sinon on extrait la racine de 3 et ensuite on divise le résultat par 2
et pas la racine carrée de 1.5
et pareil pour  (7/4)
(7/4)
D'accord, mais sur ma copie je vais l'écrire sous forme de fraction donc pas besoin de parenthèses je suppose ?
et quand tu tapes dans un logiciel de calcul aussi ...
sur le site on peut aussi utiliser le LaTeX :
utiliser les boutons LTX du bandeau du bas
ainsi que le tutoriel ![]() [lien]
[lien]
mais pour des expressions simples on a plus vite fait de les écrire "en une seul ligne" en texte avec ajout de parenthèses à bon escient
(nota : en LaTeX les "parenthèses" y seront , sous forme d'accolades, invisibles après traduction en image  )
)