Inscription / Connexion Nouveau Sujet
Variables aléatoires
**Bonjour**
Un jeu de hasard est encadrée par les règles suivantes :
- Coût d?une partie : 11 euros
- Déroulement : on tire successivement et sans remise, deux boules dans une boîte opaque contenant 2 boules blanches et n boules noires, où n est un entier naturel supérieur ou égal à 2.
- Prix : si on tire deux boules blanches on gagne 1000 euros. Si on tire 1 boule blanche on gagne 50 euros. Si on ne tire aucune boule blanche on ne gagne rien.
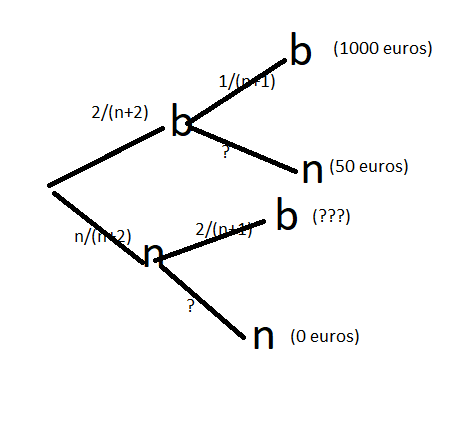
a/ Construire un arbre pondéré permettant de modéliser le jeu.
b/ Déterminer les valeurs de n pour lesquelles le jeu est : équitable? avantageux pour le joueur? avantageux pour l?organisateur.
c/ Afin de mettre en place son jeu, d?en faire la publicité et de se verser un salaire, l?organisateur estime qu?il doit obtenir 4500 euros de revenus par mois. Il souhaite savoir combien de boules noires doit comporter la boîte pour qu?il puisse espérer se générer ce revenu.
Sachant qu?il table sur 1800 parties effectuée par les joueurs tous les mois, montrer que le problème revient à résoudre l?inéquation ?8, 5n2 + 174, 5n + 1983 ? 0 puis conclure.
Bonjour je bloque sur cet exos et je n'y arrive vraiment pas. Serait il possible de me guider et de m'expliquer svp ? 
bonjour
tu sais combien on gagne si on a une boule blanche et une boule noire, mais pas si on a une boule noire et une boule blanche ? sérieux ?
et tu ne sais pas compter combien il reste de boules noires dans l'urne quand on a pris une boule blanche , sérieux ??
tu ne sais pas non plus compter combien il en reste si on a pris une boule noire ? (bon, c'est vrai que c'est plus compliqué, il faut savoir la table de soustraction de "un", au lieu de "zéro"  )
)