Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Fonctions polynômeTopics traitant de fonctions polynôme [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

variation d'une fonction

Posté par
kikipopo 23-09-21 à 16:25

Fest une fonction polynôme du second degré définie sur R par
f(x) = ax2+bx+c, où
a\varepsilon R*,
b\varepsilonR
c\varepsilonR
on suppose que a>0.
a. Utiliser la forme canonique de f pour démontrer que cette fonction admet un minimum dont on précisera la valeur ainsi que l'antécédent xm   pour lequel il est atteint.
b. Montrer que si u et v sont deux nombres réels tels que u < v \leq
xm alors f(u) - f(v)>0.
En déduire le sens de variation de f sur
]-\propto ; xm]


Aide : On se ramènera à étudier le signe de
A x (u-v) x [(u-xm) + (v-xm)]

c. Etudier de même le sens de variation de f sur
[x[sub]m[/sub] ;+\propto[
2  Etudier de même les variations de f lorsque a<0

a. le minimum est égal -b/2a et l'antécédent  est
-b(sup]2[/sup]-4ac/4a
Pour le point b. je ne  comprends pas l'aide

Posté par
kikipopore : variation d'une fonction 23-09-21 à 17:05

Pouvez-vous m'aider SVP ?
Merci

Posté par
larrechre : variation d'une fonction 23-09-21 à 17:22

Bonjour,

Commence par exprimer f(x) en faisant apparaître  xm et f(xm)

Utilise la forme canonique pour cela.

Posté par
larrechre : variation d'une fonction 23-09-21 à 17:31

Citation :
le minimum est égal -b/2a et l'antécédent  est
-b2-4ac/4a


Tu confonds image et antécédent, de plus il manque des parenthèses

Posté par
kikipopore : variation d'une fonction 23-09-21 à 17:40

la réponse que j'ai faite au point a n'est pas bonne ?
Pour moi xm correspond à -b2 - 4ac/4a et c'est l'antécédent de - b/2a

Posté par
larrechre : variation d'une fonction 23-09-21 à 17:50

Ben non, c'est le contraire, xm=-b/(2a) et f(xm)=-(b2-4ac)/(4a)

Posté par
kikipopore : variation d'une fonction 23-09-21 à 18:22

Je n'avais pas vu votre réponse précédente.
Pour les parenthèses, vous avez raison, c'est plus lisible, mais je n'en ai vu aucune dans les livres.
Pou f(u) et f(b) je remplace x par u dans un polynôme et par v dans l'autre ?

Posté par
larrechre : variation d'une fonction 23-09-21 à 18:31

Dans les livres il n'y a pas de parenthèses parce que le trait de fraction en fait office  -\dfrac{b}{2a}, mais si on écrit en ligne, il faut -b/(2a)

Ensuite, oui,  pars du polynôme sous forme canonique mais remplace -b/(2a) par xm et le minimum par f(xm) pour alléger l'écriture

Posté par
kikipopore : variation d'une fonction 23-09-21 à 19:13

(u-xm)2
(v-xm2)
j

Posté par
kikipopore : variation d'une fonction 23-09-21 à 19:19

(u-xm)2
(v-xm)2

J'avais mal placé les parenthèses

Posté par
larrechre : variation d'une fonction 23-09-21 à 19:19

Posté par
kikipopore : variation d'une fonction 23-09-21 à 19:36

Je ne vois pas ce que je dois faire

Posté par
larrechre : variation d'une fonction 23-09-21 à 19:43

Bon, j'amorce la démarche

f(x)= a(x-x_m)^2 + f(x_m) d'accord ?

En remplaçant x par u puis par v tu obtiens

f(u)=... \\ f(v)=...

Tu calcules f(u)-f(v) =...

A toi

Posté par
kikipopore : variation d'une fonction 23-09-21 à 20:59

f(u) =a(u-xm)2 +f(xm)
f(v) =a (v-xm)2 +f(xm)

f(u)=a(u-xm)(u-xm)(u-xm)(u-xm)+ f(xm)
f(v) = a(v-xm)(v-xm)(v-xm)(v-xm)
+ ​f(xm)
F(u)-f(v) = a[(u-xm)(u-xm)+f(xm)-[(v-xm)(v-xm)+f(xm)]\Leftrightarrow a(v-u) [(u-xm)+(v-xm)]

Posté par
larrechre : variation d'une fonction 23-09-21 à 21:10

Il y a des erreurs d'écritures dans ce qui précède, mais effectivement

f(u)-f(v)=a[(u-xm)2-(v-xm)2}=a(u-v) [(u-xm)+(v-xm)]

dont il faut déterminer le signe, sachant que uvxm

Posté par
kikipopore : variation d'une fonction 23-09-21 à 22:53

quand peut-on transformer une expression en  f(de cette expression) Je ne sais pas comment déterminer le signe

Posté par
kikipopore : variation d'une fonction 23-09-21 à 23:06

Bonsoir et merci.

Je reprendrai demain

Posté par
larrechre : variation d'une fonction 23-09-21 à 23:08

Citation :
quand peut-on transformer une expression en  f(de cette expression)
je ne comprends pas.

Pour le reste f(u)-f(v) se présente sous forme d'un produit de facteurs.
a0 par hypothèse

uv, donc u-v...

uxm donc u-xm...

même chose pour v-xm ...

Posté par
kikipopore : variation d'une fonction 24-09-21 à 15:12

Bonjour,
Merci de votre réponse.
Je vais reprendre mon cours et je continuerai après : le devoir est pour lundi.

Posté par
larrechre : variation d'une fonction 24-09-21 à 15:15

D'accord

Posté par
kikipopore : variation d'une fonction 26-09-21 à 21:17

Bonjour,
Pouvez-vousm'indiquer mes erreurs d'écriture du 23/09 à 20:59.
Je bloque sur cette soustraction et sur la factorisation.

Si la solution n'avait pas été dans l'exercice, je ne l'aurai pas trouvée.
Merci

Posté par
kikipopore : variation d'une fonction 27-09-21 à 11:30

onjour,
Je reprends l'exercice ;
xm = -b/2a   f(xm) = -(b2-4ac)/2a
f(x) = a(x-(-b/2a)+[-(b2-4ac/4a)]
f(x) = a(x-xm)+f(xm)
f(x) admet un minimun(a>0) en f(xm) c'est à dire en -(b2-4ac)/2a
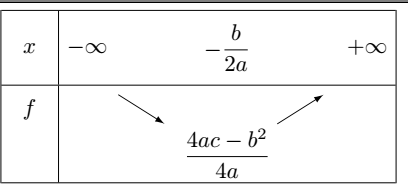
tableau de variations
x      -\propto               -xm               +\propto

f(x)                         (fxm  (c'est le minimum)    


Je ne sais pas faire  directement le tableau et les flèches  
   La flèche descends depuis l'infini jusqu'au minimum et remonte ensuite vers l'infini.
Pouvez-me dire si c'est correct ?    
Merci.        

Posté par
kikipopore : variation d'une fonction 27-09-21 à 11:35

b) xm =-b/2a     f(xm) =-(b2-4a)/4ac
f(u) = a(u_xm)2 + (fxm)

Posté par
kikipopore : variation d'une fonction 27-09-21 à 11:47

b) xm =-b/2a     f(xm) =-(b2-4a)/4ac
f(u) = a(u-xm)2 + (fxm)
f(v) = a(v-xm)2 + (fxm)
f(u)-f(v) est une identité remarquable (a-b)2 =
(a+b)(a-b)
f(u)-f(v) = a[(u-xm)-(v-xm)][(u-xm)+(v-xm)]
=a(u-v)[(u-xm)+(v-xm)]

Posté par
heklare : variation d'une fonction 27-09-21 à 11:49

Bonjour

f(x)=a\bigg(\left(x-(-\frac{b}{2a})\right)^2-\dfrac{b^2-4ac}{4a^2}\bigg)

f(x_m)= a\left(-\dfrac{b^2-4ac}{4a^2}\right) =-\dfrac{b^2-4ac}{4a}

Posté par
kikipopore : variation d'une fonction 27-09-21 à 11:57

u\leqv, donc u-v\leq 0

u\leqxm donc u-xm \leq 0


même chose pour v-xm \leq 0

Posté par
heklare : variation d'une fonction 27-09-21 à 12:07

Soient u et v deux nombres réels tels que u<v\leqslant x_m

u<v\Rightarrow u-v<0

u<x_m \Rightarrow u-x_m<0

v\leqslant x_m\Rightarrow v-x_m\leqslant0

Conclusion ?

Posté par
kikipopore : variation d'une fonction 27-09-21 à 12:12

Oui, j'ai oublié d'écrire des carrés.
Pouvez-vous me dire où je peux trouver l'outil pour écrire des fractions et  faire des tableaux de variations ?
Merci.













;

Posté par
heklare : variation d'une fonction 27-09-21 à 12:23

Pour les fractions  le plus simple (numérateur)/(dénominateur) parenthèses obligatoires

sinon les écrire en LaTeX

entre les balises tex  écrire \dfrac{numérateur}{dénominateur}

Vous avez LTX avec des points rouges comme aide

Pour le tableau  une photo en png et utilisation d'Img  voir FAQ 05

Posté par
heklare : variation d'une fonction 27-09-21 à 12:34

Mais j'ai une installation LaTeX sur ma machine

variation d\'une fonction

Posté par
kikipopore : variation d'une fonction 27-09-21 à 12:35

En conclusion la fonction est négative jusqu'à -(b2-4ac/4a)

Posté par
heklare : variation d'une fonction 27-09-21 à 12:44

La conclusion

f(u)-f(v)=a(u-v)\bigg((u-x_m)+(v-x_m)\bigg)

le premier terme est positif
les deux suivants sont négatifs donc le produit est positif


Par conséquent, f(u)-f(v) \geqslant 0 donc f(u)\geqslant f(v)

La fonction est donc décroissante sur ]-\infty~;~x_m]

Posté par
kikipopore : variation d'une fonction 27-09-21 à 12:53

si u-v<0 pour moi  ce terme est négatif

Posté par
heklare : variation d'une fonction 27-09-21 à 13:07

Bien sûr

u-v<0 et (u-x_m+v-x_m)<0 comme somme de deux termes négatifs

\underbrace{a}_{\R_+}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_-}\bigg)

Posté par
kikipopore : variation d'une fonction 27-09-21 à 13:28

Pour le point c, puisque lacourbe est une parabole, sur Xm  ; +\propto, la courbe sera ascendante,
donc u>v ; u>xm et v>xm.

Mais ce n'est pas une démonstration !


Pour le point 2
puisque a > 0, la fonction sera  croissante -\propto à xm

Posté par
kikipopore : variation d'une fonction 27-09-21 à 13:30

et décroissante de xm à +\propto

Posté par
heklare : variation d'une fonction 27-09-21 à 13:39

Sur [x_m~;~+\infty[

on repart de

\underbrace{a}_{\R_+}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_+}\bigg)

cette fois u-x_m et v-x_m sont positifs
Le produit est par conséquent négatif  donc f(u)\leqslant  f(v)

la fonction est croissante sur cet intervalle


pour la question 2 on repart toujours de l'égalité montrée à 1 b

f(u)-f(v)=a(u-v)\bigg((u-x_m)+(v-x_m)\bigg)

On étudie le signe de chacun des facteurs

Posté par
kikipopore : variation d'une fonction 27-09-21 à 14:54

Oui, je suis d'accord avec vous, mais vous pouvez écrire cela uniquement parce qu'on sait que la courbe représentative d'un polynôme du second degré est une parabole et qu'il faut donc inverser les valeurs de u, de v et xm pour que la deuxième branche de de la courbe soit ascendante.
On ne peut pas le démontrer ; on peut simplement le justifier. C'est bien ça ?

Posté par
heklare : variation d'une fonction 27-09-21 à 15:16

On ne se sert absolument pas de la courbe. Que ce soit une droite, une parabole ou n'importe quelle courbe, pour savoir si la fonction est croissante ou décroissante on se sert de la définition  C'est bien ce qui sert de démonstration

Une fonction est croissante sur I ssi pour tout u, tout v, éléments de I u<v\Rightarrow f(u)\leqslant f(v)

Pour étudier le sens de variation, on étudie donc le signe de f(u)-f(v)
NB on considère toujours u< v

Vous avez montré que  pour tout u et v réels

f(u)-f(v)=a(u-v)\bigg((u-x_m)+(v-x_m)\bigg)

Maintenant on discute

premier cas on suppose a>0 et on considère l'intervalle ]-\infty~; x_m[

  on a

\underbrace{a}_{\R_+}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_-}\bigg)

donc f(u)\geqslant f(v) donc sur cet intervalle  la fonction est décroissante

On passe maintenant à ]x_m~;~+\infty[

\underbrace{a}_{\R_+}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_+}\bigg)

donc f(u)\leqslant f(v)  la fonction est croissante sur cet intervalle

d'où en résumé le tableau 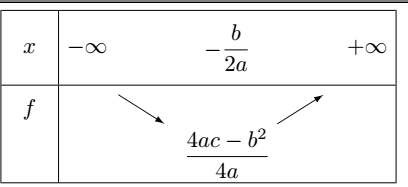variation d\'une fonction

Second cas a<0 et on considère l'intervalle ]-\infty~; x_m[

\underbrace{a}_{\R_-}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_-}\bigg)

donc f(u)\leqslant f(v) donc sur cet intervalle  la fonction est croissante

On passe maintenant à ]x_m~;~+\infty[

\underbrace{a}_{\R_-}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_+}\bigg)

donc f(u)\geqslant f(v)  la fonction est décroissante sur cet intervalle

Posté par
kikipopore : variation d'une fonction 27-09-21 à 17:42

Je ne comprends pas ce qui justifie que
[(u-xm)+v-xm)] devienne positif sur ]xm ; +\propto[

Posté par
heklare : variation d'une fonction 27-09-21 à 17:58

Si vous êtes dans l'intervalle [x_m~;~+\infty[  cela signifie que u et v sont plus grands que x_m

Il en résulte que les différences u-x_m et v-x_m  sont positives  et la somme de deux réels positifs est positive

Posté par
kikipopore : variation d'une fonction 27-09-21 à 19:52

Pour ce qui des différences, je comprends.
Mais c'est uniquement parce que je suis dans l'espace ]xm ; +\propto[que  u-xm et v-xm sont positifs ?
C'est une affirmation, ce n'est pas une démonstration.

premier cas on suppose a>0 et on considère l'intervalle
]-\propto  ; x_m[

  on a ...

donc f(u) \geqf(v)  la fonction est décroissante sur cet intervalle

Je comprends qu'il faut que  f(u) \geqf(v) pour que la fonction soit décroissante sur l'espace considéré, mais je ne comprends pas le "donc f(u) \geqf(v)"
Excusez-moi d'insister mais si je n'arrive pas à comprendre le raisonnement, je ne pas pouvoir avancer.
Merci de toutes vos explications


  

Posté par
heklare : variation d'une fonction 27-09-21 à 20:30

Si vous êtes dans l'intervalle [x_m~;~+\infty[ cela veut bien dire que tous les éléments sont plus grands que x_m

donc vous avez alors u>x_m  ce que l'on traduit aussi par u-x_m >0

c'est  utiliser la définition de la relation d'ordre  ce n'est pas une affirmation x_m<u\iff x_m-u \in \R_+


Conditions  \Large a>0\quad u\in ]-\infty~;~x_m[\quad  v\in ]-\infty ~;~   x_m [

u<v\Rightarrow u-v<0 Hypothèse   il faut bien choisir

u<x_m \Rightarrow u-x_m<0

v\leqslant x_m\Rightarrow v-x_m\leqslant0

donc (u-x_m)+(v-x_m) <0 comme somme de deux éléments négatifs

revenons maintenant à f(u)-f(v)

\underbrace{a}_{\R_+}\underbrace{(u-v)}_{\R_-}\bigg (\underbrace{(u-x_m)+(v-x_m)}_{\R_-}\bigg)

+\times -\times-=+,\qquad  f(u)-f(v) \geqslant 0  que l'on peut traduire par f(u)\geqslant f(v)

ayant montré, dans le cas où a>0,  que u<v \Rightarrow f(u)\geqslant f(v) on peut conclure que la fonction f est décroissante sur cet intervalle

Posté par
kikipopore : variation d'une fonction 27-09-21 à 20:48

Merci beaucoup.
Je vais tout reprendre et je vais chercher un autre exercice du même genre.
Bonne fin de journée.

Posté par
heklare : variation d'une fonction 27-09-21 à 21:01

N'hésitez pas  si vous avez des questions ou besoin d'éclaircissements.
De rien
Bonne fin de soirée

Posté par
kikipopore : variation d'une fonction 27-09-21 à 21:03

Merci


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !