Inscription / Connexion Nouveau Sujet
variation et limites d'une fonction
Bonsoir,
j'ai un petit exercice à réviser et j'ai oublié comment on fait pour le résoudre :/
Si quelqu'un pourrait m'aider ça serait sympa ^^'
La fonction f est définie sur R par :
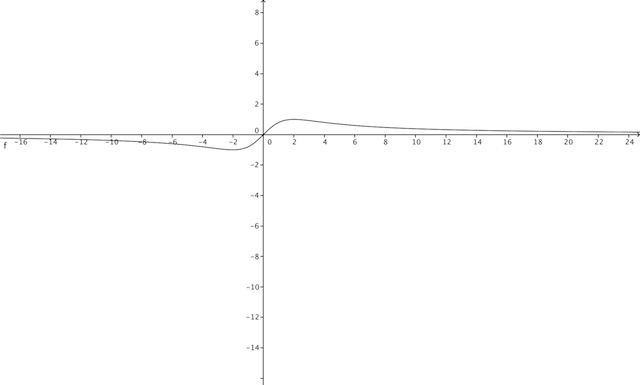
f(x)=4x/x²+4
1) Etudier les variations de f sur R.
2) Déterminer ses limites en +oo et -oo
3) Tracer la courbe représentative de f dans un repère orthonormal.
4) Quelles sont les valeurs prises par f(x) lorsque x décrit l'ensemble R ?
Merci d'avance à la personne qui m'aidera .
Merci Labo, j'essaye de le faire et jte l'envois pour que tu me dises si c'est bon okey ?
Togodumnus, il s'agit de la deuxième 
D'accord. Dans ce cas-là, applique la relation donnée par Labo.
Je vous laisse donc, c'était simplement pour éviter une éventuelle confusion. 
Labo je trouve (4-2x)(4+2x)/(x²+4)²
C'est bon ?
Par contre, dans le tableau de signe, je mets quoi entre -oo et +oo ?
OK pour la dérivée
s'annule pour x=2 et pour x=-2
tu fais un tableau de signe ou tu appliques le théorème du signe d'un trinôme...
f'(x)>0 pour -2<x<2
Moi dans mon tableau j'ai une ligne avec x
la suivante avec 4-2x (qui s'annule pour 2)
en dessous une autre avec 4+2x (qui s'annule en -2)
en dessous encore une autre avec (x²+4)²
apré en colonne bah j'ai mis -oo ; -2 ; +2 ; +oo
C'est correct pour l'instant ?
Bonjour
le signe de f' est su signe du numérateur puisque le dénominateur est un carré positif, non nul
d'où le tableau:
Ouais j'ai compris merci 
Mais maintenant comment faire pour avoir les limites en -oo et +oo ?
Merci.
Par contre je n'ai plus de pile sur ma calculatrice et j'aimerai bien avoir l'allure de la courbe pour la question
3) Tracer la courbe représentative de f dans un repère orthonormal.
Merci encore à toi (: !
Merci beaucoup ! Tu pourrais m'aider sur la dernière question ^^'
4) Quelles sont les valeurs prises par f(x) lorsque x décrit l'ensemble R ?
Merci encore à toi!