Inscription / Connexion Nouveau Sujet
Vecteurs colinéaires avec Trigo
Bonjour ! Petit exo d'un Dm de maths qui me pose problème =
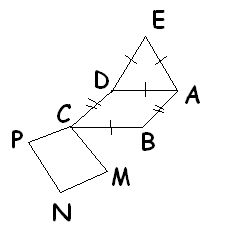
Il faut montrer que les vecteurs AE et NP sont colinéaires et de même sens.
On sait que :
- ADE est un triangle équilatéral,
- ABCD est un parallèlogramme et ( AD , AB ) = 
/6
- CMNP est un parallèlogramme et ( CD , CM ) = - /2
[ Pour démontrer que 2 vecteurs u et v sont colinéaires, il faut prouver que
(u,v) = 0 mod 2 si u et v ont le même sens ou que
(u,v) = mod 2 si u et v sont de sens opposés.
Donc les vecteurs u et v colinéaires 
(u,v) = 0 mod ]
Merci de la future réponse 
bonsoir et bienvenue p3rhaps 
(joli pseudo !)
1 règle d'or : 1 topic = 1 exo .
Je reponds au premier ici . Copie-colle le second dans un autre topic pour avoir une correction.
Calculons donc l'angle (AE,NP)
en utilisant Chasles:
(AE,NP) = (AE,AD) + (AD,DC)+(DC,CM)+(CM,NP)
= (AE,AD) + (-DA,DC) + (-CD,CM)+ (CM,NP)
et voyons chaque angle separement:
(AE,AD) = pi/3 car triangle equilateral et sens direct
(DA,DC) est dans un parallelo. L'angle contigü vaut pi/6 . la somme des angles du parallelo valant 2pi, celui ci fait donc 5pi/6 . Comme il est en sens indirect ,l'angle orienté vaut -5pi/6
donc (-DA,DC) = pi+(DA,DC) = pi-5pi/6 = pi/6
(CD,CM)= -pi/2
donc (-CD,CM) = pi-pi/2 = pi/2
CMNP étant un parallélo, les vecteurs CM et NP sont de sens opposé et donc (CM,NP ) =pi
ajoutons tout ceci:
(AE,NP) = pi/3 +pi/6 +pi/2 + pi = 2pi
voili voilou!
Merci beaucoup Sarriette
Enfin une réponse
Je copie-colle l'autre tout de suite !
Annuler
connectez vous