Inscription / Connexion Nouveau Sujet
Vérification de mon tableau de signe
Bonsoir  pourriez vous me dire si mon tableau de signe est correct ?
pourriez vous me dire si mon tableau de signe est correct ?
f(x)= (-3x^2 + x + 4) / (2x^2 - 7x + 3)
J'ai calculé Delta pour ces deux équations du second degré, et en les plaçant dans le tableau voilà ce que j'obtiens : (mais le résultat de f(x) dans le tableau ne me semble pas correct...) Merci beaucoup
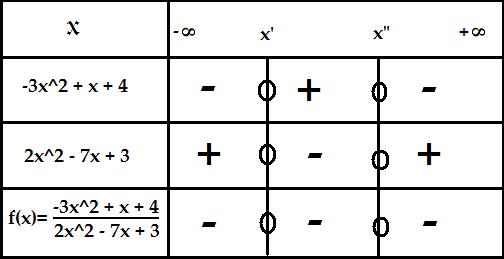
Bonsoir ... A vue de nez, ce n'est pas correct ...
Il faut donner sa place à chacune des racines du 1er polynôme, et du second polynôme ...
Il ne faut pas oublier de mettre les doubles barres aux Zéros du dénominateur .
Merci de me répondre,
D'accord donc il faut que je donne la place à chaque racine de chaque polynôme et ne pas oublier les doubles barres au dénominateur.
Mais par contre si je veux faire ça il faut que je factorise les deux polynômes non?
Johnny,
Quand je calcule delta d'un polynôme, comme delta est supérieur à 0 il y a deux solutions.
x' et x" permettent d'obtenir ces deux solutions 
Yota, je m'étonne de ta remarque... A ton niveau , tu devrais voir que les racines ne sont pas les mêmes ...
Bonsoir!
Mais dans cette function t'as deux polynomes. Donc il y a (au maximum) 4 racines (2 pour le numérateur, et 2 pour le dénominateur). Les deux racines du dénominateur sont des singularités. Il faut factoriser les deux polynomes (numérateur et dénominateur).
ton tableaux sera qqchose comme:
x1 x2 x3 x4
-3x^2 + x + 4 - 0 + 0 -
2x^2 - 7x + 3 + 0 - 0 +
f(x) - 0 + // - 0 + // -
avec // = indéfinie
Dans mon exemple x1 et x3 sont les racines du numérateur, et x2 et x4, celles du dénominateur.
Bon courage!
Oui je sais les calculer grâce à delta...
Le problème est peut être que je ne sais pas vraiment comment présenter mon tableau


