Inscription / Connexion Nouveau Sujet
Volume d'un bol
Voila un exercice, je suis coincée au début alors si vous pouviez m'aider!...
Nous avons un bol ayant la forme d'un paraboloïde de révolution. Ce solide est obtenu par rotation de l'arc de parabole d'équation y=x2 pour 0 x
x 1 autour de l'axe des ordonnées.
1 autour de l'axe des ordonnées.
On se propose de calculer le volume V de ce solide. Soit un entier n 1; on partage ce solide en n tranches horizontales T1, T2,..., Tn hauteur 1/n.
1; on partage ce solide en n tranches horizontales T1, T2,..., Tn hauteur 1/n.
1)Soit i un entier compris entre a et n. On désigne par vi le volume de la tranche Ti, située entre la hauteur (i-1)/n et i/n.
a)Vérifier que le rayon R du cercle situé à la hauteur i/n est tel que R2=i/n.
b)En encadrant Ti entre 2cylindres, pour tout entier i compris entre 1 et n, démontrer que:
( (i+1))/n2
(i+1))/n2 vi
vi (
( i)/n2
i)/n2
En déduire que:
( (1+2+...+(n-1)))/n2
(1+2+...+(n-1)))/n2 V
V (
( (1+2+...+n))/n2
(1+2+...+n))/n2
paraboloïde de révolution:
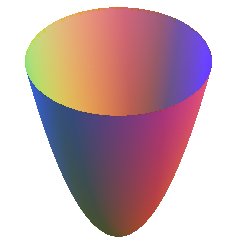
ce n'est que lé début de l'exercice, j'ai prouver la 1ere question graphiquement, le b) jai prouver la 1ere partie mais je ne sais pas en déduire la suite, alors si quelqun pouvait m'aider ce serait sympa! Merci =)
2) Pour tout entier n 1, on pose:
1, on pose:
an=( (1+2+...+n))/n2
(1+2+...+n))/n2
a)Démontrer que que, pour tout entier n 1:
1:
V an
an V+(
V+( /n)
/n)
En déduire que la suite (an) converge vers le réel V.
b)Démontrer que, pour tout entier n 1:
1:
an=((n+1) )/2n
)/2n
En déduire la valeur de V.
Si jamais la suite de l'exercice vous inspire plus^^
si y=i/n le rayon c'est le x= rac(i/n) donc R²=x²=y=i/n
et le petit cylindre de hauteur ((i+1)/n-i/n) de rayon R apour volume 1/n* *i/n=1/n²*
*i/n=1/n²* *i,
*i,
le petit cylindre de hauteur ((i+1)/n-i/n) de rayon R'=rac((i-1)/n) apour volume 1/n* *(i-1)=1/n²*
*(i-1)=1/n²* *(i-1),
*(i-1),
tu additionnes les cylindres "majorants"  *((1+2+...+n))/n²
*((1+2+...+n))/n²
tu additionnes les cylindres "minorants"  *((0+1+...+(n-1)))/n²
*((0+1+...+(n-1)))/n²
or ((1+2+...+n))=n*(n+1)/2.... continue.... je dois quitter


