Inscription / Connexion Nouveau Sujet
Volume d'un cylindre surmonté d'un tronc de cône
Bonjour à tous !
J'ai un petit souci avec un exercice pour un dm.
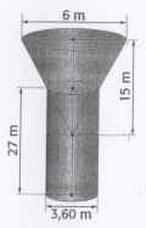
Un château d'eau a la forme d'un cylindre surmonté d'un tronc de cône contenant un réservoir d'eau.
1. Calculer le volume du cylindre.
2. a) calculer le volume du cône non tronqué.
b) calculer le volume de la partie tronquée du cône
c) en déduire que le tronc du cône a un volume égal à 35.28  m3
m3
3. le réservoir d'eau est une réduction du tronc de cône à l'échelle 9/10
calculer, puis donner le volume d'eau que contient ce réservoir à 1 litre près
----------------------------------------------------------------------------------
1.  x 1.80(au carré) x 27
x 1.80(au carré) x 27
87.48
274.826 m3
2a)  x 3(au carré) x15
x 3(au carré) x15
135
424.115 m3
et après je ne sais plus....
Déjà pouvez-vous me dire si la partie tronquée c'est bien celle qui est à l'intérieur du cylindre ?
De plus je ne vois pas comment trouver la hauteur du cône à l'intérieur du cylindre...
Pouvez-vous m'expliquer comment faire je ne suis pas très douée en géométrie....
Merci par avance
Pour la question 1 ok
Pour la question 2 je trouve pas pareil:
2a
Voici la formule:
V=(1/3)*B*h
Avec B aire de la base
B=Pi*R^2
V=(1/3)*Pi*R^2*h
V=(1/3)*Pi*3^2*15
V=45Pi
V=141.37
2b
Voici la formule:
V=(h/3)*(B+b+(racine(Bb))
Avec B et b aire des la base
B=Pi*R^2
B=Pi*3^2
B=Pi*9
b=Pi*R^2
b=Pi*1.8^2
b=Pi*3.24
Tu remplace dans la formule mais d apres ton dessinon a pas h !
h est different de 15 !
on veut la hauteur de la partie superieur (ou ca s agrandi)
Merci alaknanda
Désolée pour le 2a) j'avais juste oublié de diviser par 3.... quand je vous dis que je suis pas douée !
Pour la formule que tu m'as donné :
V=(h/3)*(B+b+(racine(Bb)) jamais vu cela..... la formule m'est complètement inconnue !!!
De plus la hauteur h est inconnue... comment faire pour la trouver ?
Merci par avance
Bonlour Véro ... Tu es toujours au travail sur ce devoir ?...
Si oui, où en es-tu ?... je vois qu'on t'a conseillé des formules un peu en dehors du cours ...
alors on peut faire le point ?...
Bonjour jacqlouis
Désolée, je viens de rentrer et de voir ton message !
Oui je suis toujours sur ce devoir ! C'est vrai que la formule que m'as donné alaknanda, je ne l'a connais pas...
Et en plus je ne vois pas coment trouver la hauteur ?
et une deuxième chose qui me tracasse est-ce que la partie tronquée du cône est bien la partie qui est dans le cylindre ?
Si tu pouvais m'expliquer ; ce serait avec grand plaisir !
Tu le demandes si gentillement !...
Considère le cône , en le retournant; ce sera peut-être plus clair...
C'est donc un cône de base circulaire (R=3) et de hauteur h=15 .
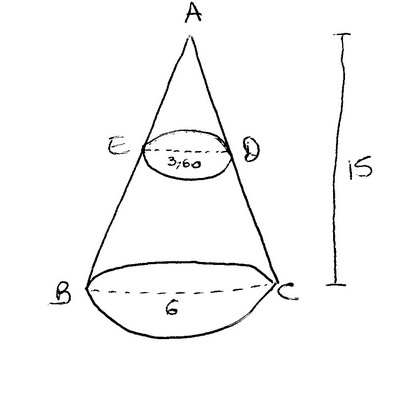
Une partie (le haut) est supposée être dans le cylindre, le reste est la partie visible. Si on représente le cône entier par un triangle (tu peux le tracer sur ton brouillon) , la base aura donc 6 m de diamètre, et la hauteur 15 m. Vers le milieu de la hauteur, tu traces un diamètre intermédiaire, de 3,60 m (à la séparation cylindre-cône).
D'après Thalès, on aura ; 3,60 / 6 = h / H (h étant la hauteur de la partie invisible) . Comme H =15, on trouve facilement h = 9 m .
Est-ce que je suis assez clair ?
Merci de ton aide !
oui tu es clair mais par contre j'ai pas tout compris... Si on suit le théorème de Thalès
on obtient : AE/AB = AD/AC = ED/BC
je ne savais pas que l'on pouvait incorporer les hauteurs h/H
Ca je ne l'ai jamais vu...
Tu ne l'as jamais vu !... Cela m'étonne ...
Si tu coupes ton triangle par une hauteur partant du sommet, et passant par les centres des cercles , les diamètres des cercles BC et ED restent parallèles: donc on a encore AE/AB = AO'/AO = EO'/BO ...
J'ai appelé AO' = h , et comme EO' = 1,8 et BO = 3 ... h = 9 . OK ?
Ok Ok j'ai compris mais il faut m'expliquer longtemps !!!!
Donc maintenant que j'ai les hauteurs
Pour le 2 b) il faut que je calcule le volume du cône qui est la partie dans le réservoir (partie tronquée)
2 c) la partie visible du cône
Calcule d'abord (et sans faire d'erreur, comme plus haut ! )le volume de TOUT le cône .
Tu peux donner la valeur exacte, puisque on te demande ensuite la valeur exacte du tronc de cône.
Après j'ai calculé le volume du "petit" cône
V = (1/3) x Pi x R^2 x h
V = (1/3) x Pi x 1.8^2 x 9
V = 9.72 Pi
V = 30.5362 m3
45*Pi Oui... (je t'avais dit valeur exacte)
Maintenant que tu as le volume V du cône entier, tu peux calculer le volume V1 de la partie supérieure (cachée dans le cylindre) dont tu connais hauteur (h) et rayon (1,80) . On a donc pour volume exact : ...
le volume V1 (partie supérieure)
V1 = (1/3) x Pi x R^2 x h
V1 = (1/3) x Pi x 1.8^2 x 9
V1 = 9.72 Pi
V1 = 30.5362 m3
Le volume V2 (partie supérieure)
V2 = V - V1
45 pi - 9.72 pi = 35.28 pi
110.8353 m3
Oui, c'est bien cela ... mais les décimales sont tout-à-fait incongrues dans ces calculs , où les données de base n'ont que DEUX chiffres significatifs ...
Merci de ta patience ! C'est gentil !
J'ai encore un petit souci avec le 3) pourquoi une échelle à 9/10 ?
Je ne vois pas ce qu'il faut faire !!!
Puis-je encore te demander ton aide ?
Pourquoi 9/10 ? probablement, parce que la cuve est costruite en béton assez épais, et l'on estime que le volume intérieur est égal aux 9 / 10 du volume extérieur ...
Connaissant l'extérieur, tu peux facilement et directement en déduire l'intérieur , rien qu"en connaissant le coefficient de réduction, ici 9/10 .
Réfléchis avant de m'envoyer ta réponse ...
Soit V' = Volume intérieur
V' = V x (9/10)au cube
V' = 141.37 x 729/1000
V' = 103.058 m3
1 m3 = 1 000 l
103.058 m3 = 103508 litres
Dommage ... mais bravo quand même . Tu as évité le piège !...
Mais tu aurais dû prendre le volume du tronc de cône, qui est le réservoir d'eau...c'est-à-dire les 35,28 m3 pour base du calcul ...
et pas trop de décimales ...
Je viens de refaire avec les bons chiffres (du moins je l'espère)...
V' = V x (9/10)au cube
V' = 110.83 x 729/1000
V' = 80.79 m3
1 m3 = 1 000 l
80.79 m3 = 80790 litres
C'est très bien... Tu as même enlevé des décimales ... (mais en fait en arrondissant , je pense que cela donne 80,80 m3 , mais ce n'est pas grave ! )
Je te remercie vraiment de tes explications !
C'est super sympa d'avoir passé du temps à m'aider ! 
Mille mercis encore
Bonne soirée
veroww


