Inscription / Connexion Nouveau Sujet
Volume d'une boite en fonction de x
Bonjour à tous, voici mon problème :
On veut construire le patron d'une boîte de lait dans une feuille carrée de 30 cm de côté.
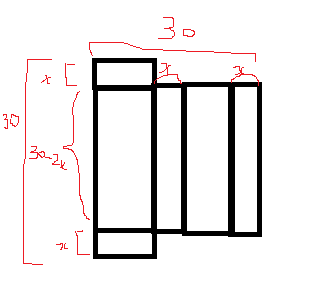
La figure 1 (à gauche) représente ce patron et la figure 2(à droite) est celle de la boite qui est un parallélépipède rectangle.
Question : Exprimer en fonction de x le volume V(x) de la boite.
Je suis presque sûr que la réponse est x(30-2x)² mais je ne peux pas le prouver.
Merci à tous !

Salut,
Le volume est égal au produit des trois dimensions de la boîte.
Tu en as une : c'est x.
Il te faut les deux autres : hauteur et profondeur.
pour la hauteur, t'as pas une idée ?
Bonjour,
Tu sais que le volume d'un parallélépipède rectangle est donnée par la formule : , où L désigne la longueur, l la largeur et h la hauteur.
Ici, on peut voir que la largeur du parallélépipède rectangle vaut x (voir image de droite)
Sa hauteur est égale à 30-2x (d'après image de gauche)
Sa longueur est plus compliqué à calculer : On a .
Ainsi le volume est égale à :
.
Je te joins une image pour que tu puisses y voir plus clairement.
Et donc, si on développe, qu'est-ce que cela pourrait donner ? Je pensais qu'en développant, nous allions retomber sur la dérivée de la fonction dont nous devions étudier le signe au début
Quelqu'un pourrait m'aider à trouver à quel intervalle appartient alors x ?
]0;30] ? ]0;30[ ? Autre ?
Bonjour, je rencontre des problèmes dans le développement de l'équation pourriez vous m'aidez ?
cordialement.
je rencontre des problèmes dans le développement de l'équation
montre précisément ce qui t'ennuie
je trouve au final 2x^3-30x^2+30x or précédemment il fallait étudier 2x^3-60x^2+450x et je me demande si mon équation du volume est bonne.
Désolé pour l'écriture.
voici mon équation
** image supprimée *![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
** image supprimée **
je suis d'accord avec l'expression qu'on doit trouver et qu'on t'a fait étudier auparavant
quelles sont les dimensions de ta boîte ? (les échanges au dessus ne sont pas nécessairement justes !! )
et quelle est l'expression de ton volume ?
Ainsi, si je comprend bien, mon équation de départ est fausse ?
Dans ce cas, quelle est-elle puisque même après m'y être creusé les méninges, je ne la trouve pas.
Merci pour vos réponses rapides.
Bonjour,
- peut être lire l'ensemble de la discussion et pas seulement le premier message
- et donner tes calculs = les recopier, pas les photographier.
Bonjour j'ai le même énoncé et, de plus c'est l'équation du quatrième message que j'ai utilisé.
Quant à l'énoncé le voila : on veut construire le patron d'une boite de lait dans une feuille carré de 30 cm de côté
Les valeurs sont les mêmes que l'énoncé du dessus
"le quatrième message" c'est "up" le 11-04-12 à 17:53, il n'y a aucune formule dedans. 
(il y a des dates et des heures à chaque message)
et rien ne t'empêche de toute façon plutôt que de nous obliger à aller fouiller au dessus et compter les messages de recopier ta formule de départ et tes calculs
sans ça personne ne peut rien pour toi à part te dire que le calcul correct à partir de la formule correcte donnerait le résultat correct point barre.
Bon je pense que l'on va s'arrêter là et que je vais trouver sans votre aide jusqu'ici peu précieuse. En effet je n'aime pas la condescendance que vous utilisez pour me parlez alors que je suis la seulement par besoin d'aide et suis, jusque là, resté poli.
Bonne soirée.


