Inscription / Connexion Nouveau Sujet
maximum et minimum d'une fonction
Bonjour je voudrez savoir comment peut on faire pour calculer le minimum et le maximum d'une fonction , dont la courbe n'est pas une parabole?
f(x)=9x/(x²+2x+4)
Merci d'avance!!
"technique" et non "teccnique" !!
Donc on va essayer de montrer que f(x)  9/2
9/2
puis de montrer que f(x)  3/2
3/2
Attends , j'ai dit : "on va essayer" !!
Tu veux bien faire les calculs de ton côté et moi du mien. Le 1er qui trouve le met sur le site.
On commence par :
montrer que f(x)  -9/2
-9/2
Si on peut montrer que f(x) est tjrs  -9/2 , c'est que son minimum est -9/2.
-9/2 , c'est que son minimum est -9/2.
Tu ne comprends pas ça ? Un minimum veut dire que f(x) ne peut pas prendre une valeur plus petite que -9/2(=-4.5) par exemple -5 .
Si on peut montrer que f(x) est tjrs  3/2 , c'est que son maximum est 3/2.
3/2 , c'est que son maximum est 3/2.
Un maximum veut dire que f(x) ne peut pas prendre une valeur plus grande que 3/2(=1.5) par exemple 2.
Ce que tu proposes est bon et tu écris maintenant :
9x/(x²+2x+4)+9/2  0
0
Avant, il faudrait dire que le déno x²+2x+4 n'est jamais nul ( discriminant négatif) donc f est définie sur  .
.
Il ne faut pas oublier que ma question de départ avec cette fonction était de trouver par le calcul que le maximum est 3/2 et le minimum est -9/2 
Après réduc au même déno qui est 2(x²+2x+4) et qq. petits calculs , on arrive à :
9(x+2)²/2(x²+4x+4)  0
0
Le déno est positif car il n'a pas de racine donc est du signe du coeff de x² qui est 1.
Le nulé est tjrs positif ou nul car c'est un carré.
Donc on a bien :
9(x+2)²/2(x²+4x+4)  0
0
Donc :
f(x)  -9/2
-9/2
et -9/2 est son minimum.
Tu montres que f(x)  3/2 toute seule et tu me l'envoies si tu veux. OK ?
3/2 toute seule et tu me l'envoies si tu veux. OK ?
Moi, je vais faire un autre exo.
Desole mais je né pas compri cette partie de l'explication pouver vous me la reformuler svp
Quelle partie ?
non c'est bon jai compri vos explication  mais je ne comprend pas en quoi
mais je ne comprend pas en quoi
f(x)-3.2 0 et f(x)+9/2
0 et f(x)+9/2 0 prouve que -9/2
0 prouve que -9/2 f(x)
f(x) 3.2((cela est une autre maniere dencadrer la fonction entre son minimum et maximum))
3.2((cela est une autre maniere dencadrer la fonction entre son minimum et maximum))
D'abord , tu remarqueras que (j'ai corrigé des fautes de frappe) :
f(x)-3/2 0 donne : f(x)
0 donne : f(x)  3/2
3/2
et f(x)+9/20  0 donne : f(x)
0 donne : f(x)  -9/2
-9/2
Cela veut dire que f(x) est "coincé" entre -9/2 et 3/2. Tu n'écris pas ça !!
Mais tu peux écrire :
Donc :
-9/2  f(x)
f(x) 3/2
3/2
ce qui prouve que -9/2 est le mimimum de f(x) et 3/2 son maximum.
Pas clair, ça ?
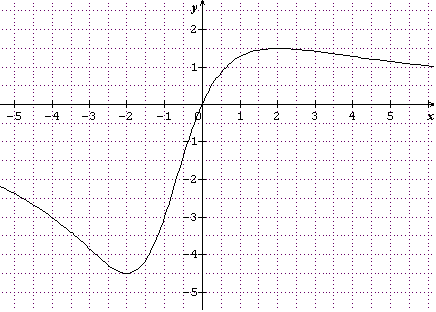
Puis regarde la courbe que je t'ai envoyée . Je te rappelle que les valeurs de f(x) se lisent sur l'axe des y.
Tu vois bien que les valeurs de f(x) sont "coincées" entre -4.5 et 1.5.
Ok merci beaucoup je pense avoir compris , je vous souhaite une bonne fin de journée et à bientôt peut etre
, je vous souhaite une bonne fin de journée et à bientôt peut etre
(( en ce moment je suis en train de faire un exercice sur les barycentre aussi et jespere que si je "galere", je peux compter sur vous ))
))
merci !! de votre aide
Dans ton énoncé sur les barycentres , il n'y a pas une faute de frappe à la 1)
.....=||vec MB+2vecMB||.
car à droite on aurait 3 vect MB.