Bonjour Jasmine

Dans ta liste tu as écrit deux fois (1;3;2). Les autres commençant par 1 sont justes. Tu les comptes, et tu en trouves 12. Tu es d'accord que 1 ne joue aucun rôle particulier dans cette histoire, donc il y en a ausi 12 qui commencent par 2, puis 12, par 3 et par 4 et par 5... au total . Donc si tu ne trouves que 50 c'est... que tu en oublies!

En fait ce que tu écris là, c'est exactement l'arbre tel qu'on te l'a expliqué plus haut!

waah!

Ah bonjour Camélia!:)

ah je suis si contente d'avoir de l'aide de la part des correcteurs! C'est la première fois!


Ah je comprends! D'accord!
Je vais revoir toutes mes réponses, est-ce que vous pourriez les vérifier?

S'il vous plait.

Oui, bien sur... Je te suis depuis longtemps mais maintenant tu rentres dans mon domaine de compétence... Je suis très mauvaise pour les collégiens!

Ah oui?

temps mieux, je suis lycéenne

Donc,

a. L'événement "obtenir au total au nombre de trois chiffres" est constitué de 12*5 issues donc 60/120=0.5

b. Quelle es la probabilité d'obtenir un nombre n'ayant que des chiffres impairs?

L'événement "obtenir un nombre n'ayant que des chiffres impairs" est constitué de 12*3 issues donc 36/120=0.3
Pour l'instant, je réponds correctement?

a) Il y a bien 60 issues, mais je ne vois pas trop d'où tu sors le 120.

b) Là je ne suis pas d'accord. Pour n'avoir que des chiffres impairs, il faut tomber à chaque fois sur 1,3, ou 5. Il y a donc 3 possibilités pour le premier, 2 pour le suivant et il ne reste qu'une boule impaire... Ca fait 6 issues favorables en tout... faciles à écrire: (1,3,5), (1,5,3), (3,1,5), (3,5,1) (5,1,3) et (5,3,1)

ah?

120 c'est toutes les issues sans exceptions.
dans mon cours, on présente à chaque fois le résultat sous forme décimal

Pour la b, d'accord je comprends, donc on donc faire 6*3 non? car il y a 3 possibilités et 6 issues.
18 issues .

mais on doit le mettre sous forme décimal.

Quelque chose m'échappe. C'était quoi le début de l'exo? Pour moi avec 3 tirages il y en tout et pour tout 60 issues. Parmi celles-ci, seulement 6 sont formées de nombre impairs. je ne vois toujours pas le 120!

ah c'est sa l'énoncé, je n'ai rien oublié
bon vous avez raison alors
et comment fait-on pour mettre notre résultat sous forme décimal?

Bon alors en enlevent le 120 je reprends mes réponses:

1)

a. L'événement "obtenir au total au nombre de trois chiffres est constitué de 12*5 issues donc la probabilité est:{60}

b. L'événement "obtenir un nomnbre n'ayant que des chiffres impairs" est constitué de 12*3 issues donc la probabilité est: {36}

c. Quel est l'événement contraire de l'événement précédent(question 1b)? Quelle est sa probabilité?


L'événement contraire de l'événement précédent est "obtenir un nombre n'ayant que des chiffres pairs".

C'est mieux comme sa?

Bonsoir,
Je me permets,

ah bonsoir Ted

Oui justement, c'est pour sa que je ne comprends pas, normalement c'est 60/120=0.5 et 120 c'est toutes les issues sans exceptions c'est à dire sans

Tu tires successivement et sans remise trois boules dans une urne qui en contient 5 :
comme les tirages sont successifs, il y a un ordre et comme il est effectué sans remise on peut dire que l'on cherche à déterminer le nombre d'arrangements de trois boules parmi 5, comme je ne sais pas si tu as déjà vu les arrangements on peut raisonner autrement.
pour la première boule tu as 5 choix possibles
pour la deuxième plus que 4 choix possibles
enfin pour la troisième restent trois choix
il y a donc 5*4*3=60 manières de tirer trois boules successivement et sans remise.

oui

donc pour les autres je fais 36/60 et non 36/100

les autres quoi ? quelle question ?

ah oui désolée

b. 36/60=0.6

Comment arrives tu as 36 issues possibles ?
tu as trois boules portant un chiffre impair  :
donc 3 choix possibles pour la première
2 choix pour la deuxième
1 choix pour la troisième
ce qui fait 3*2*1 choix possibles pour obtenir un nombre composé uniquement de chiffres pairs, voici l'arbre :

Bonjour

ah oui j'ai compris

Donc 6 possibilités, 6/60=0.1

pour la c, ma phrase est-elle correct?

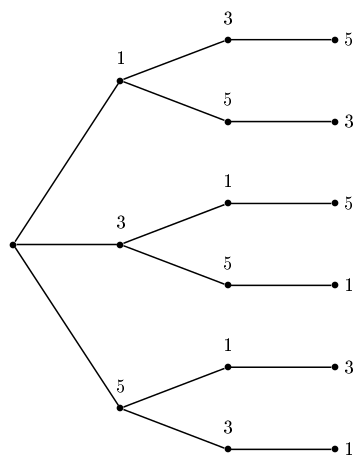
L'évènement contraire d'obtenir que des chiffres impaires et l'évènement "obtenir au moins 1 chiffre pair"

Bonjour

hein?

Vous êtes sûr? C'est bizarre on dirait même pas son contraire

Bon je ne vous demande pas comment sa se fait, sinon on va en mettre du temps.

Si c'est au moins un chiffre impair alors on prends toutes les issues et on a toutes les chances d'obtenir le 3 le 5 ou le 1.
5*3*2*1
30/60=0.5

tout les chiffres sont impairs donc "un n'est pas impair" est le contraire
si un n'est pas impair ça veut dire qu'au moins un est pair...
le contraire de tout est au moins un
que le contraire de pour tout est il existe au moins un

ah j'ai compris!

C'était un peu embrouillant!

donc, si on tire trois boules, on peut trouver des chiffres impairs OU pairs.
Donc, là il y a tout les chiffres non?

quand on te dit "on tire trois boules" on considère tous les cas possibles
que des pairs, que des impairs, un mélange des deux

oui, mais là c'est une exception
On veut au moins un chiffre impair donc au moins un 1, un 3 ou un 5.
ah je crois comprendre, on a 1 chance sur 3 d'avoir un chiffre impair c'est bien sa?

c'est toujours pareil :
au premier tirage 1 impairs parmi 3 donc 3 choix
au deuxième tirage deux choix possibles
au troisième tirage plus qu'un choix possible
Il faut te mettre dans le contexte que tu veux obtenir à l'issue de tes trois tirages. En général l'énoncé te donne le contexte.

ah mais pourquoi on dit qu'il y a 5 boules alors?

je ne comprends pas où tu veux en venir :
il y a 5 boules dans l'urne
on fait un tirage sans remise de trois boules
on veut trois boules impaires
il y a trois boules impaires dans l'urne
donc tu te mets dans le contexte  d'obtenir trois boules impaires :
tes tirages de trois boules impaire se fait parmi les cinq boules de l'urne mais tes tirages favorables doivent se faire parmi les trois qui sont impaires.

Mais peut-être que je ne comprends pas ta question ...

ah d'accord

bon alors l'événement contraire de l'événement précédent est "obtenir un moins un nombre impair". Sa probabilité est 3*2*1=6/60=0.1

c'est pas le contraire de tous impairs que tu veux ? donc au moins 1 pair ?
tu peux passer par l'évènement contraire 1-p(tous impairs)

ah oui c'est vrai! En plus on l'indique dans mon cours! Suis-je bête!

1-0.1=0.9

ok mais soigne ta rédaction ... là tu balances un résultat mais si c'est un travail à rendre ça passeras pas

Ah oui biensûr!

Regardez ma rédaction:
1)
a. L'événement  "obtenir au total au nombre de trois chiffres" est constitué de 12*5 issues soit 60 issues possibles.

b. L'événement "obtenir un nombre n'ayant que des chiffres impairs" est constitué de 3*2*1 issues. Sa probabilité est 6/60=0.1

c. L'événement contraire de l'événement précédent est "obtenir un moins au nombre impair".
En utilisant le calcul de probabilité d'un événement contraire on a : 1-p(tous impairs)=1-0.1=0.9

d. L'événement "obtenir un nombre n'ayant que des chiffres pairs" est constitué de 4*2 issues. Sa probabilité est :8/60=0.13

Décidément c'est vous qui m'aider encore une fois, je vous remercie

tu vas pas me maudire ...
tu connais la distinction entre nombre et chiffre ?
un nombre est composé de chiffres, tu dois donc te corriger ...

J'ai fait la deuxième partie toute seule.

2)
On tire maintenant au hasard successivement trois boules en les remettant dans la boîte après chaque tirage. Chaque tirage étant fait "au hasard", la loi de probabilité de cette expérience aléatoire est l'équiprobabilité.

a. L'événement "obtenir au total un nombre de trois chiffre" est constitué de 15*5 issues possibles soit 75 issues.

b. L'événement "obtenir au nombre n'ayant que des chiffres impairs" est constitué de 3*3*3 issues. Sa probabilité est 9/75=0.12

c. L'événement contraire de l'événement précédent est "obtenir au moins un nombre impair".
En utilisant le calcul de probabilité d'un événement contraire on a : 1-p(tous impairs)=1-0.12=0.88.

d. L'événement "obtenir un nombre n'ayant que des chiffres pairs" est constitué de 5*2 issues. Sa probabilité est : 10/75=0.13

c. L'événement contraire de l'événement précédent est "obtenir au moins un nombre (im)pair".
En utilisant le calcul de probabilité d'un événement contraire on a : 1-p(tous impairs)=1-0.12=0.88. ===> 1-0.1=0.9 ?

non la je suis sur la deuxième partie

la première partie, c'est correct non? Je l'ai fini

désolé j'avais sauté quelques messages
alors pour la première partie ok voyons la deuxième partie :
étant donné qu'après chaque tirage tu remets la boule dans l'urne tu as à chaque tirage 5 choix possibles donc : combien de tirages possibles ?

pour la b) je suis d'accord avec le nombre d'issues 3*3*3 comme le nombre de tirages possibles n'est pas 75 la probabilité va changer

pour la c) l'évènement contraire de "obtenir trois chiffres impairs" est "au moins un chiffre pair) donc tu devras faire 1-p(obtenir 3 impairs)

pour la d) deux boules portant un chiffre pair, on remet la boule après chaque tirage donc ?*?*? issues possibles...

Bonjour

Désolée de répondre si tard.

Oui il y a bien 5 choix possibles, je crois que je me suis trompée, j'avais mis 15 issues possibles et fait 5*15=75.

Mais non, il y a 120 issues possibles car on prends toutes les issues, 5*4*3*2*1=120.

Je reprends mes réponses car tout change.

b) 3*3*3=9/120=0.075
c) 1-p(tous impairs)=1-0.075=0.925
d)5*2=10/120=0.083

Bonjour,

il restait 5 et c'était correct!

oui mais ce n'est pas le même raisonnement avec ton calcul :
5*4*3*2*1 c'est un tirage de 5 boules sans remise alors que nous on tire trois boules avec remise ce n'est pas la même chose :
dans un tirage sans remise chaque tirage, de par son résultat, à une influence sur le tirage suivant
alors qu'un tirage avec remise n'a pas d'influence pour le tirage suivant puisque le contenu de l'urne ne change pas.

oui, tout à fait.
pour les probas, il faut bien comprendre chaque mot de l'énoncé car c'est là dessus qu'on se base. Si on l'a mal compris toutes nos réponses sont fausses.

Dites, pour la 1a) et 2a), est-ce qu'on peut réprésenter l'univers sous forme de tableau ou arbre? Ou bien ce n'est pas nécessaire?

Tu peux le faire si tu veux : mais ça te prendra de la place ...

Est-ce que, si vous seriez un professeur de mathématiques, vous auriez demander à votre élève "pourquoi n'avez-vous pas mis un schéma à arbre ou un tableau?" ?
Et l'auriez-vous donné tous ces points ?