Inscription / Connexion Nouveau Sujet
Intersection d'une droite et d'une parabole ?
Bonsoir,
Je nage un peu dans mon DM, et j'aurais besoin de votre aide pour éviter que je me noie complètement.
Voici dans un premier temps l'énoncé :
" Le plan est rapporté à un repère orthogonal. Le réel m étant fixé, on définit la droite dm d'équation y=2x+m . On considère la parabole P d'équation y=x²+6x+6 . "
Puis les questions :
"1) A l'aide du graphique, déterminer pour quelles valeurs de m la droite dm et la parabole P ont :
a) deux points d'intersection ;
b) exactement un point d'intersection ( dont on donnera les coordonnées ) ;
c) aucun point d'intersection."
Bien sûr, voilà le graphique :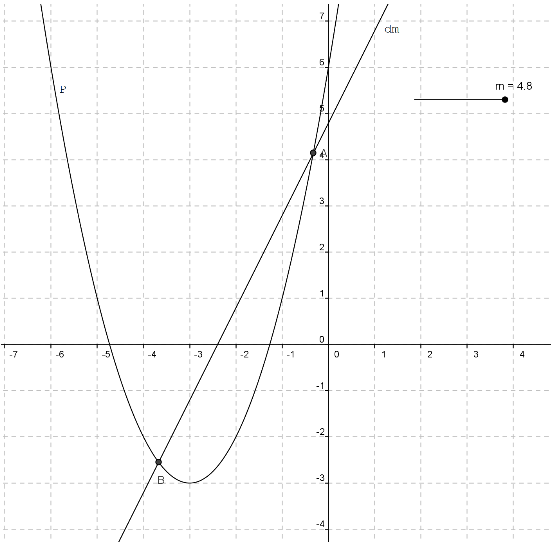 
* Tom_Pascal > image récupérée localement, redimensionnée, puis placée sur le serveur de l'
... tout ça pour toi, merci d'utiliser l'outil d'attachement des images du forum et de suivre les consignes la prochaine fois Akira-Kane *
Celle-là, j'y ai répondu, alors voilà mes réponses :
a) Lorsque m > 2 , dm et P semblent avoir deux points d'intersections ;
b) Lorsque m = 2 , dm et P semblent avoir exactement un point d'intersection de coordonnées ( -2 ; -2 ) ;
c) Lorsque m < 2, dm et P semblent n'avoir aucun point d'intersection.
Et enfin, la question qui suit :
"2) Retrouver par le calcul les résultats obtenus à la question 1."
Et là, je n'y arrive qu'avec m = 2 :
Si m = 2 :
x² + 6x + 6 = 2x + 2
x² + 4x + 4 = 0
( x + 2 )² = 0
x + 2 = 0
x = -2
Pour trouver y , on remplace x par -2 dans une des équations :
y = (-2)² + 6 * (-2) + 6 = 4 - 12 +6 = -2
Donc l'intersection de dm et P a pour coordonnées ( -2 ; -2 ).
Mon problème en fait, c'est que je ne sais pas comment m'y prendre pour répondre au a) et au c). Il faut bien utiliser x² + 6x + 6 = 2x + m ... ? Mais comment, vu qu'on sait juste que m > 2 ou m < 2 ?
Merci d'avance,
Akira.
Fais le calcul des solutions avec m, puis regarde ce qu'elles deviennent lorsque m est supérieur, puis inférieur à 2.
A Tom_Pascal : Vraiment désolée, je pensais plus pratique de mettre l'image sous un lien, mais apparemment je me suis trompée. Je ferai attention.
Pour en revenir au DM :
Ahem, je ne suis pas sûre d'avoir bien compris ...
Faire le calcul des solutions avec m ?
Je dois donc utiliser simplement "m" ?
Ca me conduirait alors à :
x² + 6x + 6 = 2x + m
x² + 6x + 6 - 2x - m = 0
x² + 4x - m + 6 = 0
... Mais en fait j'ai l'impression que ce que je viens de faire ne sert absolument à rien.
Soit on s'est mal compris, soit je ne sais pas/plus faire. x)
Une petite précision, ou un exemple, enfin une quelconque aide serait super, merci.
J'obtiens alors :
Delta = b² - 4ac
= 4² - 4 * 1 * ( 6 - m )
= 16 + 4m - 24
= 4m - 8
Et là je résous m = 0 ; m > 0 ; et m < 0 ?
4m - 8 = 0 4m - 8 > 0 4m - 8 < 0
4m = 8 4m > 8 4m < 8
m = 2 m > 2 m < 2
Euh ?
( Je viens de remarquer que j'ai dit une petite bêtise : ce n'est pas m = 0 ; m > 0 ; et m < 0 , mais plutôt Delta = 0 ; Delta > 0 ; et Delta < 0. )
En tout cas merci beaucoup pour ton aide Priam, et bon, pour conclure, j'ai lu dans un autre topic que tu avais écrit :
Suivant que le discriminant sera, en fonction des valeurs que peut prendre le paramètre p , positif, nul où négatif, l'équation aura deux solutions, une solution double ou pas de solution réelle. Il y aura alors deux points d'intersection, un point double ou aucun point d'intersection.
( Je farfouille un peu partout, oui. En tout cas ça me sert. )
Merci encore pour ton aide, et Bonne soirée !
j'ai un exercice du même type mais je bloque après la résolution de delta
serait il possible que l'on m'aide?
cordialement
Akira-Kane
Priam
bonjour Louise59
tu dis que tu as un exercice du même type.
si ce n'est pas exactement le même énoncé, je te conseille d'ouvrir un nouveau topic,
d'y recopier ton énoncé intégralement.
si c'est exactement le même énoncé que celui en cours,
qu'entends-tu par "je bloque après la résolution de delta " ?
ce discriminant delta, selon qu'il va être négatif, nul ou positif,
va te permettre de déterminer le nombre de points d'intersection entre la parabole P et la droite Dm
(i.e. le nombre de solutions de l'équation selon la valeur de m)
étudie donc séparément chacun de ces 3 cas.
la question, telle que posée ici, ne demande pas les coordonnées des points d'intersection, juste combien il y en a.
Annuler
connectez vous