Inscription / Connexion Nouveau Sujet
Déverrouiller une tablette tactile
Bonjour à tous,
En observant une tablette tactile, je me suis demandé comment la déverrouiller, ou plutôt, combien de combinaison à tester existait.
Pour la déverrouiller, il faut tracer un schéma sur ce fond:
[img1]
On doit tracer des segments entre les différents points sans lever le doigt.
Le schéma est donc composé d'au moins un segment, et d'un maximum de 8.
L'ordre dans lequel on joint les points a une importance. Par exemple, joindre le point central au point situé en haut à gauche ne déverrouille pas la tablette si le schéma attendu joint le point situé en haut à gauche au point central.
De plus, il est impossible d' "éviter" un point. Par exemple, si l'on tente de joindre le point du haut au points du bas, on passe obligatoirement par le point central.
Les segments peuvent se croiser et on peut joindre des points en utilisant des diagonales.
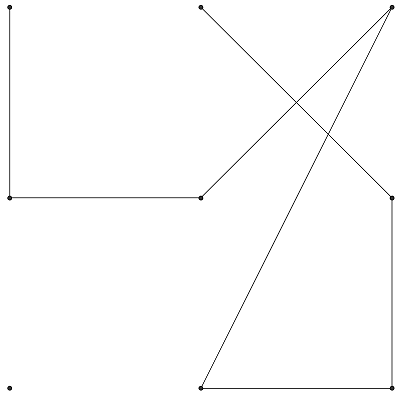
Voici par exemple un schéma possible:
[img2]
Ma question est donc: Combien de schémas différents existent ?
Bonjour,
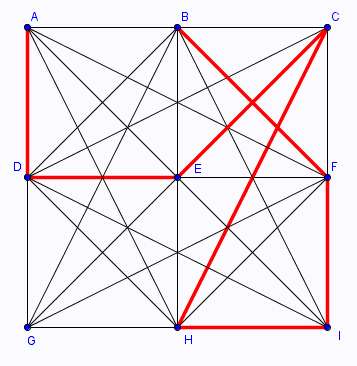
Pour bien vérifier où on va :
Il s'agit donc de dénombrer tous les chemins possibles sur ce graphe
reliant deux points donnés du graphe, et ce pour tous les choix de points donnés ?
Déja pour le choix des deux points on a 9*8 = 72 choix possibles.
Pour chacun de ces choix, il faut dénombrer tous les itinéraires reliant A et B
Il y aura exactement autant de chemins A B que de chemins B
B que de chemins B A, on peut se contenter des 72/2 = 36 choix non ordonnés des deux points, et multiplier par deux le résultat.
A, on peut se contenter des 72/2 = 36 choix non ordonnés des deux points, et multiplier par deux le résultat.
par symétries, on peut se contenter des choix
A-B
A-C
A-E
A-F
A-I
Le problème va donc être de compter ces chemins...
Il va y en avoir un sacré gros paquet !!
Bonjour mathafou,
Tu as parfaitement saisi le problème, il y a vraiment beaucoup de possibilités!
Ma première idée a été de résoudre le problème progressivement:
J ai essayé de réduire le nombre de points a 2, 3,4 ou 5 pour compter plus facilement le nombre de possibilités. Ensuite, j'ai espéré qu'une sorte de suite logique apparaisse, une sorte de formule qui donnerait en fonction de la disposition des points et de leur nombre le nombre de possibilités. Cela aurait permis de généraliser et de resoudre le problème qui nous intéresse.
Mais je n'y suis malheureusement pas parvenu. 
Ton idée de limiter les possibilites a prendre en compte grâce aux symétries est vraiment bonne ! 
Mais malgré tout, il reste un grand nombre de chemins.
N'existe-t-il pas des formules en théorie des graphes qui permettrait de comptabiliser des chemins en fonction du nombre de noeuds et d'arêtes?
Bonjour,
Il y a des tas de choses en théorie des graphes concernant les dénombrements.
Le problème est que il s'agit essentiellement d'algorithmes et non de formules, même itératives.
Il est "facile" de dénombrer tous les chemins d'un point A à un point B sur un graphe
Il l'est beaucoup moins quand on impose la contrainte de ne pas passer deux fois sur le même sommet !
Cette contrainte n'est pas explicitement indiquée ici :
un chemin tel que A-E-F-B-E-C est il autorisé ?
voire même le cas extrème un chemin A-B-A ??
Le principe de l'algorithme pour trouver les chemins si on acepte les répétitions :
On écrit la matrice M du graphe, Mij = 1 si arc entre sommet i et sommet j, 0 sinon (et Mii = 0)
On calcule M², M3, M4 ... Mk ...
Chacune donne le nombre de chemins en exactement k arcs entre sommet i et sommet j, pour tous les couples i,j d'un coup.
Si on fait la somme M + M² + M3 + M4 ...+ Mn on obtient le nombre de chemin en au plus n arcs entre i et j
Il suffit alors de faire la somme de tous les termes de cette matrice pour avoir notre résultat.
Ici le calcul jusqu'à la puissance 8 d'une matrice 9 9 ne devrait pas effrayer un ordinateur bien dressé...
9 ne devrait pas effrayer un ordinateur bien dressé...
le plus pénible est d'écrire la matrice M :
[0,1,0,1,1,1,0,1,0],
[1,0,1,1,1,1,1,0,1],
[0,1,0,1,1,1,0,1,0],
[1,1,1,0,1,0,1,1,1],
[1,1,1,1,0,1,1,1,1],
[1,1,1,0,1,0,1,1,1],
[0,1,0,1,1,1,1,1,0],
[1,0,1,1,1,1,1,0,1],
[0,1,0,1,1,1,0,1,0]
On flanque ça dans Maxima, Mathematica, Mapple etc, ce que vous avez sous la main.
On obtient la matrice du nombre de chemins en au plus 8 arcs M + M² + .. + M8 =
((((((M.M + M).M + M).M + M).M + M).M + M).M + M).M + M
[ 281782, 352547, 281782, 352547, 400237, 352547, 332962, 352547, 281782 ],
[ 352547, 444900, 352547, 444815, 504209, 444815, 417421, 444900, 352547 ],
[ 281782, 352547, 281782, 352547, 400237, 352547, 332962, 352547, 281782 ],
[ 352547, 444815, 352547, 444900, 504209, 444900, 417421, 444815, 352547 ],
[ 400237, 504209, 400237, 504209, 571660, 504209, 473703, 504209, 400237 ],
[ 352547, 444815, 352547, 444900, 504209, 444900, 417421, 444815, 352547 ],
[ 332962, 417421, 332962, 417421, 473703, 417421, 393629, 417421, 332962 ],
[ 352547, 444900, 352547, 444815, 504209, 444815, 417421, 444900, 352547 ],
[ 281782, 352547, 281782, 352547, 400237, 352547, 332962, 352547, 281782 ]
on fait la somme de tous les termes : 31799815
sauf erreur de calcul ou erreur dans le graphe.
Avec répétitions autorisées. Il y en donc moins si on interdit de repasser deux fois au même sommet.
Donc finalement ça fait pas tant que ça ...
Voilà un joli calcul! 
Je pense avoir saisi l'idée de représenter les connexions entre les noeuds par une matrice puis d'additionner différentes matrices (M², M 3 ... M k).
Quand on les ajoute, on additionne leurs termes de même rang?
Mais je crois qu'il va encore falloir affiner le calcul car malheureusement, on ne peut pas passer 2 fois par le même sommet (je viens d'essayer... ).
).
Autre remarque: J'ai dit qu'il était ipossible d'éviter un point, mais il y a une sorte de cas particulier. En règle générale, il est impossible de tracer le segment A-C sans passer par B. Mais si le point B est déjà utilisé dans le schéma, alors on peut en quelque sorte passer par dessus lui.
Exemple: Il est possible de tracer le schéma B-D-A-C, ou même B-A-C sans que les segment AC passe par B, car il est déjà utilisé.
Au moins, on sait qu' il y a moins de 31799815 possibilités, c' est toujours ça! 
Remarque: Si on pouvait passer plusieurs fois par le même point, on pourrait faire des schémas infinis du type A-B-A-B-A-B-...!
Le schéma est donc composé d'au moins un segment, et d'un maximum de 8.
donc non, on ne peut pas faire un schéma infini, c'est dans l'énoncé.
C'est pas que c'est impossible, c'est seulement interdit

Mon calcul matriciel s'arrête à M8 à cause de cette contrainte là : longueur maxi 8.
si on a le droit de continuer il faudrait ajouter M9, M10, etc... jusqu'à l'infini.
ce qui évidemment donne un résultat infini, du simple fait de l'existence de circuits dans le graphe.
Aussi :
1) oui. quand on ajoute deux matrices A et B on ajoute chaque terme de même "rang"
C = A+B c'est Cij = Aij + Bij pour tous les i,j
Le produit est plus compliqué à définir. Avec le produit vient l'élévation au carré etc.
2) "on sait qu'il y a moins de 31799815 possibilités"
En fait on ne sait plus rien du tout.
puisque le graphe change au fur et à mesure qu'on avance en rajoutant ou non les arcs A-C, A-I, A-G, B-H, C-G, C-I, D-F, G-I selon qu'on est ou non passé déja par B,D,E,F,H ou pas...
Bref on ne peut même plus tracer un graphe statique...
Pas tout à fait.
Tout ceci a tout de même permis de préciser les règles du jeu !
S'il est interdit de repasser sur le même sommet, cela diminue beaucoup le nombre de chemins !
Une majoration plus intéressante est alors de considérer plutôt que le graphe est complet. C'est à dire qu'on a aussi toujours le droit de faire A-C etc...
Chaque sommet étant relié à chacun des 8 autres.
Alors le nombre de chemins sans répétitions de sommets dans ces conditions se calcule beaucoup plus simplement que sur un graphe tordu (incomplet) :
nombre de chemins de 1 arc 9*8
nombre de chemins de 2 arcs 9*8*7
nombre de chemins de 3 arcs 9*8*7*6
nombre de chemins de 4 arcs 9*8*7*6*5
nombre de chemins de 5 arcs 9*8*7*6*5*4
nombre de chemins de 6 arcs 9*8*7*6*5*4*3
nombre de chemins de 7 arcs 9*8*7*6*5*4*3*2
nombre de chemins de 8 arcs 9*8*7*6*5*4*3*2*1
total apres factorisation et réorganisation :
(((((((1+1)*2 + 1)*3 + 1)*4 + 1)*5 + 1)*6 + 1)*7 + 1)*8*9 = 986400
Comme certains arc sont parfois interdits il y aura moins de 986400 combinaisons.
Combien est une autre histoire ... (à cause du parfois)
C' est déjà bien comme majoration!
Des idées en vrac:
Pour un arc, aucun chemin n'est interdit.
Pour 2 arcs, il y a sauf erreur de ma part, 16 chemins interdits a cause du fait qu'on ne peut pas éviter un point. De plus, si AB est le premier arc, alors le deuxieme arc ne peut pas etre AB. Pour un arc donné cela elimine donc une possibilité. MAIS ces chemins interdits peuvent l' être pour les 2 raisons à la fois!
Tous les chemins interdits pour 2 arcs le sont pour 3 (en ajoutant un arc). Les chemins interdits supplémentaires sont ceux pour lesquels le troisième arc rejoint un point ayant déjà ètè utilisé.
De manière générale, si un chemin a n arcs est interdit, alors un chemin qui le prolonge avec d'autres arcs est interdit également.
Mais je ne sais pas si ça aide beaucoup à préciser le "parfois"...