Inscription / Connexion Nouveau Sujet
La coupe est pleine
Bonsoir à tous 
Un problème apparemment très simple .
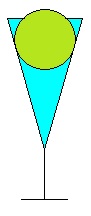
Un verre conique est plein à ras bord . On place une bille à l'intérieur de façon à évacuer le maximum de liquide . Quel doit être le rayon de la bille ( en fonction des caractéristiques du cône ) ?
Amusez-vous bien 
Imod
PS : blankage à éviter .
Bonjour!
J'essaie de trouver sans calcul et sans rigueur.
J'improvise.
Faisons croître le rayon r de la bille à partir de 0.
Pour r petit, la bille est complètement immergée.
le volume d'eau qu'elle évacue est égal à son propre volume.
Il grandit donc avec r, jusqu'à ce qu'elle soit complètement immergée mais tangente à la surface. Cette première phase est donc réglée.
Suit une phase plus mystérieuse où r grandit jusqu'à ce que la bille soit tangente au bord du haut du verre. Pour r encore plus grand, elle plonge de moins en moins dans l'eau et en chasse de moins en moins.
Cette phase ultime est donc réglée.
Reste la phase intermediaire mysterieuse.
Soit r le rayon de la bille.
Donnons à r l'accroissement infinitésimal dr.
Pour mesurer la difference d'eau chassée, il me semble , intuitivement, qu'il revient au même de ne pas toucher à la bille et de baisser de dr le niveau de l'eau dans le verre.
La surface de l'eau est délimitée par deux cercles concentriques.
Je pense qu'il va falloir faire des calculs.
Suis-je sur la bonne voie?
Bonsoir,
Il serait utile de donner des dimensions pour une étude concrète.
Pour le moment j'ai pris la même méthode que rogerd
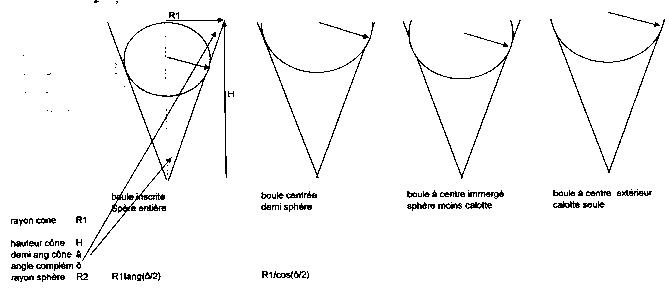
1/La boule imérgée totalement la plus grande (cercle inscrit ) donne environ 50 %
2/dans les boules "posées" on voit vite que les grosses laissent une calotte
sphérique inférieure à la boule 1/
3/il semble que l'idéal soit une boule posée centrée sur le diamètre du haut du cone
On va phosphorer encore
Bonjour Roger et re pour dpi
Je pense avoir trouvé le rayon vidant le maximum de liquide . Le rayon ne dépend pas vraiment de la forme du cône c'est pour cette raison que je n'ai pas donné de dimension .
La solution semble simplissime mais je ne comprends pas la logique qu'elle cache .
Imod
>imod
Je pense qu'un îlien va tomber sur ton topic et le résoudre.
Pour avancer,je donne quelques élèments:
Ton dessin doit être dans le vrai,par contre je doute de la longueur des cotés donnée dans ton autre topic (sauf cas particulier).
Dans mon exemple R=3 et H=8 ,je trouve:
volume du cône 75.4
1/volume d'une boule totalement immergée 37.4 soit liquide résiduel 37.8 de l'ordre de la moitié.
2/boule tangente avec centre sur base du cone
rayon 2.809 volume total 92.84 volume évacué (demi sphère ) = 46.4
volume résiduel 29 c'est donc mieux
3/ton dessin donnerait une sphère de 2.9 de diam dont une calotte
resterait extérieure ,avec un volume de 47.1 déplacé ,elle aurait
donc la palme,
4/si on regarde les sphères avec des rayons supérieurs on perd
en volume car les calottes extérieures progressent plus vite
Tout cela pour dire qu'il doit y avoir une belle courbe R,r,H à trouver
J'ai pris mon stylo et j'ai commencé les calculs ( dans le cas où le centre de la bille est à l'extérieur du verre ) et bizarrement ce n'est pas trop compliqué .
Je note :
R : le rayon de la bille .
H : le hauteur du cône .
X : la profondeur du pôle sud de la bille .
â : le demi angle du cône .
Le volume de la calotte immergée est proportionnel à X²(3R-X). Comme sin â=R/(R+H-X) , on a R=(H-X)sin â/(1-sin â), on remplace dans le volume de la calotte et on obtient que ce volume est proportionnel à X²(2Xsin â + X -3Hsin â ) qui est une fonction de X . Cette fonction atteint son maximum quand X=2sin â/(1+sin â ) ( il suffit de dériver ) et alors R=Hsin â/[(1-sin â)(1+2sin â)]
C'est bien le résultat annoncé sur l'autre site .
Je n'ai pas vérifié si le calcul était le même avec le centre inondé 
Imod
>imod
J'ai essayé ta formule dans mon exemple cela donnerait une
spère de rayon 2.54 donc centre immmergé puisque les positions
sont:
R> r* cos â : calotte sphérique seule
et R < r cos â : sphère -calotte extérieure (avec limite à r tang ( /2-â )
/2-â )
*r =rayon de la "base" du cône
J'ai fait le calcul avec le centre immergé et j'arrive encore à la formule à la même formule .
@dpi : je n'ai pas vraiment compris ton message précédent , tu as un contre-exemple pour le rayon proposé ? En tout cas merci pour ton intérêt 
Il reste à regarder l'histoire du trapèze mais ça devrait pouvoir attendre demain.
Imod
Bonjour,
à noter que le volume d'une calotte est valable que h soit < ou > au rayon ...
et même si c'est une "tranche" de sphère :
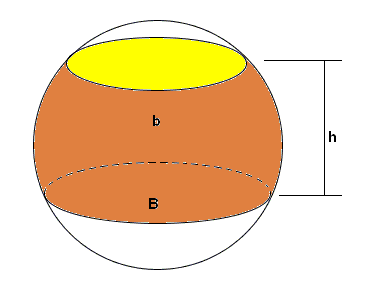
(formule extraite du Petit Larousse !)
où B et b sont l'aire des deux sections circulaires et h l'épaisseur de la tranche
pour une calotte à part entière b = 0 et on a
où h est la hauteur de la calotte et B l'aire de la section.
ce qui explique que tu trouves un résultat (formule) identique que le centre soit immergé ou pas.
Nota :
désolé j'ai peint après coup par remplissage de zone ce qui est impossible si les traits sont dessinés avec "antialiasing" (flou volontaire pour donner l'illusion de traits nets en juxtaposant des pixels) : le "flou volontaire" est basé sur le fond blanc d'origine et donne des bords "pleins de blanc" lors du remplissage. mais bon, c'est pas pour publier non plus ...
Il y a quelque chose qui ne colle pas dans ta formule Larousse, Mathafou (il suffit d'examiner un ou deux cas particuliers).
Je ne sais pas où j'ai bien pu aller chopper mon 4/3, sans doute sur la formule d'à côté
c'est
OK, j'ai donc dû la redémontrer du coup, avec ce doute :
le dernier terme vient de l'identité A3 - B3 = (A-B)3 + 3AB(A-B)
maintenant les aires des deux faces sont d'où on tire
ce qui donne en remplaçant dans V :
CQFD
Bonjour
>mathafou
J'espère qu'en voyant mes définitions du 05/03 10h08
tu ne doutes plus de l'égalité éventuelle entre le rayon de la
base (ou du sommet ) du cône ,de sa hauteur et du rayon de la
fameuse sphère .
.
>imod
As-tu travaillé avec R1 ?
Bonjour,
à dpi, justement si !! en voyant tes définitions du 05/03 10h08 c'est là que j'ai tiqué sur R1 = H = R2
ces définitions indiquent le contraire de ce que tu affirmes, puisqu'elles sont "générales" !!
il faut remonter plutôt au post du 03-03-13 à 19:43
Le rayon ne dépend pas vraiment de la forme du cône
pour se permettre d'affirmer que "on se place dans le cas particulier où H = R1"
affirmation que je n'ai pas vraiment comprise d'ailleurs (pourquoi cela ne dépendrait pas de la forme du cone) mébon je n'ai pas réfléchi en profondeur à ce problème non plus...
Après des calculs, et des erreurs de calcul, et sans faire aucune hypothèse sur la position (émergée / immergée) du centre de la boule, je confirme, s'il en était besoin, la formule de Imod :
J'ajoute que cela correspond à une position immergée du centre de la boule (X étant, comme le dit joliment Imod, la profondeur du pôle sud de la boule)
Bonjour à tous
J'encourage vivement les participants
à voir sur le site communiqué le message 5548
qui est interactif ..
Dpi , je crois que tu fais référence à un dessin de JLT , le numéro que tu donnes est le nombre de messages que JLT a envoyé et comme il est bavard 5548 est dépassé depuis longtemps 
C'est vrai que les images animées et la qualité du latex ( je ne parle pas de celle des participants ) est un véritable atout des mathématiques.net mais je vais arrêter de faire de la pub pour les autres sites 
Ce qui est sûr c'est qu'il reste encore pas mal de choses à dire sur ce problème .
Imod
Bonjour,
Dans tous les cas de figure, le rayon de la bille qui évacue le plus d'eau est
où ,
et
sont respectivement la génératrice, le rayon et la hauteur du cône.
En effet, pour , le volume évacué est
Une étude de cette fonction montre qu'elle est toujours strictement croissante sur l'intervalle .
La borne inférieure de cet intervalle est dictée par la fait pour, que un rayon inférieur, la bille serait complètement immergée, donc évacuerait de moins en moins d'eau lorsque décroît.
La borne supérieure tient au fait que, pour un rayon supérieur, la partie immergée de la bille est de moins en moins grande au fur et à mesure que croît.
Bien cordialement,
Je relis les messages précédents :
- rogerd avait réalisé une bonne analyse du problème
- Imod avait précisé que la forme du cône importe peu,
mais la figure qu'il donne ne correspond pas à ma solution dans laquelle la bille qui évacue le plus d'eau
est tangente à la surface latérale du cône le long du cercle de la base :
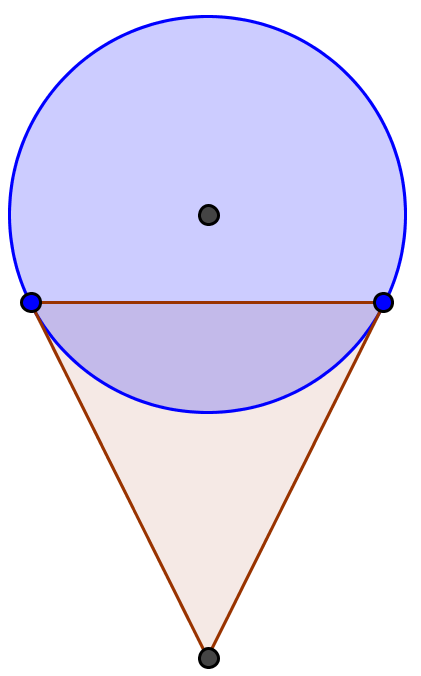
Une petite correction : lorsque la bille est complètement immergée, elle n'évacue évidemment pas d'eau du tout !
(maudite pub)
La solution est donnée,mais la meilleure démo est
donnée dans la maison (site)indiquée par imod 07/03 2316, sous
le message 5548 avec une figure où l'on voit toutes
les positions en faisant varier un seul point..
J'ai l'impression que tu fais erreur, Pierrecarre.
Je n'en vois pas une raison simple et évidente, mais j'en suis déjà "moyennement convaincu" à l'oeil : voir le dessin ci-dessous.
En outre , ton expression du volume concerné, de dimension 4, est un peu bizarre.
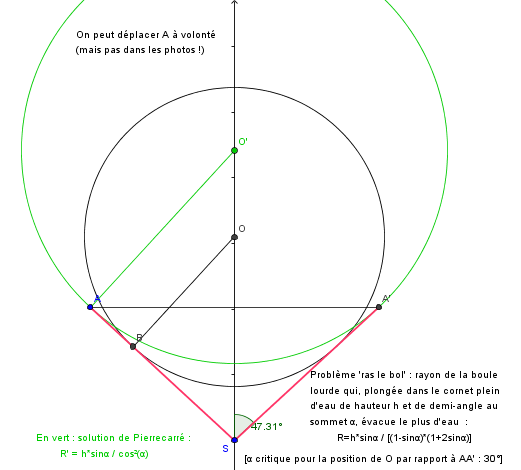
Certes, je me suis planté : une erreur de signe dès le départ !
Plus, un deuxième message farfelu.
Je rectifie donc :
La conclusion : quelle que soit la forme du cube, le maximum d'eau évacuée se réalise pour
On peut même étendre la fonction sur l'ensemble des réels positifs :
et voir que celle-ci est continue et dérivable partout.
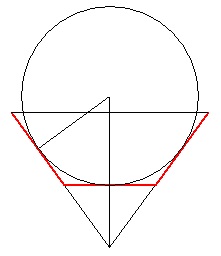
On peut démontrer le quadrilatère est un trapèze isocèle dont les côtés latéraux ont la même longueur que la base, ce qui permet d'obtenir une construction géométrique de la bille qui évacue le maximum d'eau :
- tracer la bissectrice de ;
celle-ci coupe en
;
- construire le milieu de
;
- par , mener la perpendiculaire à SA ;
celle-ci coupe la demi-droite en
.
La bille a pour centre et pour rayon
.
Pour DPI : rien ne t'oblige à lire ceci.
En procédés de démonstration, je ne suis par sûr que certains soient " meilleurs " que d'autres.
Chaque manière de démontrer a sa raison d'être et les différentes manières d'arriver à un résultat font la richesse des mathématiques.
C'est vraiment dingue : on pense " cône " et on écrit " cube " (mais cela ne change rien aux calculs !)
Bonjour,
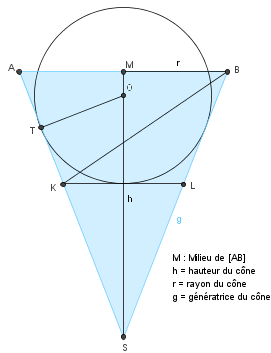
voici l'illustration du raisonnement d'Imod
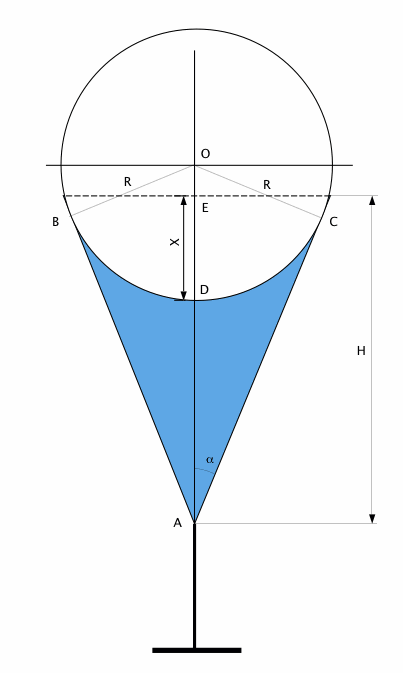
le volume déplacé correspond à la calotte sphérique de hauteur DE ( X) soit
Vd =  /3* DE2*(3R- DE) ou
/3* DE2*(3R- DE) ou  /3*X2*(3 R - X)
/3*X2*(3 R - X)
D'un autre côté, on a R = OA*sin où OA = R + H -X
où OA = R + H -X
On peut voir que R= ((H-X)*sin )/(1-sin
)/(1-sin )
)
En remplaçant R par cette valeur dans l'expression de Vd
on trouve Vd=  /(3*(1-sin
/(3*(1-sin ))*X2*(3H*sin
))*X2*(3H*sin -2X*sin
-2X*sin -X)
-X)
En annulant la dérivée soit 2Hsin -X*(2sin
-X*(2sin +1=0, on trouve la valeur de X qui donne un maximum de volume Vd soit
+1=0, on trouve la valeur de X qui donne un maximum de volume Vd soit
X = 2Hsin /(2sin
/(2sin +1)
+1)
La valeur de R qui en découle est R=H sin /(1- sin
/(1- sin )
)
Examinons le cas particulier de  =30° avec sin
=30° avec sin =1/2
=1/2
et prenons par exemple H=10cm
(La figure 2 illustre ce cas)
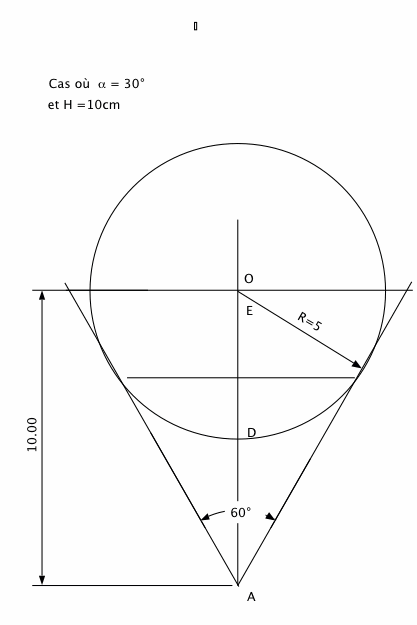
X = 5cm et R = 5cm
Le centre de la sphère se trouve dans le plan supérieur du verre
C'est vraiment trop sympa d'avoir détaillé et illustré ce que j'avais proposé 
Personnellement je m'interroge toujours sur le trapèze à trois côtés égaux , il y a forcément une explication simple à cette solution mais je n'arrive pas à mettre le doigt dessus 
Merci Castoriginal 
Imod
Personnellement je m'interroge toujours sur le trapèze à trois côtés égaux , il y a forcément une explication simple à cette solution mais je n'arrive pas à mettre le doigt dessus