Fiche de mathématiques
Ile mathématiques > maths 2nde > Géométrie
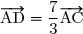
2. Construire la parallèle menée par C à (DB).
Cette parallèle rencontre (AB) en G.
3. Calculer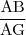
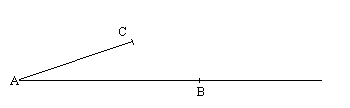
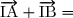
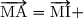
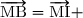
En déduire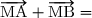
2. Prouver que, s'il existe un point M tel que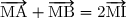 alors I est le milieu de [AB].
alors I est le milieu de [AB].
3. Compléter :
Conclusion :
I est le milieu de [AB] si et seulement si
12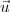 - 48
- 48 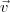 + 5
+ 5 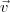 =
=
8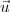 + 3
+ 3 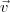 - 5(
- 5(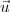 -
- 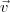 ) =
) =
3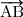 +
+ 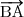 +
+ 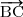 -
- 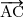 =
=
2. Que peut-on dire des points M et N dans les cas suivants ?
3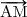 = 3
= 3 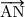
3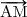 = 2
= 2 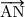
3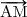 = - 3
= - 3 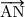
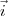 ,
,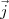 ,
,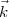 ) .
) .
1. Calculer les coordonnées du vecteur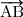 .
.
2. Calculer les coordonnées du vecteur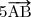 .
.
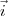 ,
,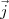 ,
,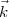 ).
).
Le vecteur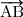 a pour coordonnées (2 ; 1 ; 5) dans la base (
a pour coordonnées (2 ; 1 ; 5) dans la base (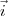 ,
,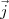 ,
,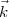 ).
).
Quelles sont les coordonnées du point B ?
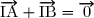
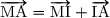
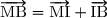
Donc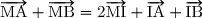
2. D'après la question précédente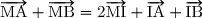 .
.
Si nous avons un point M tel que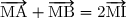 alors
alors 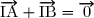 , donc I est le milieu de [AB].
, donc I est le milieu de [AB].
3. Conclusion :
I est le milieu de [AB] si et seulement si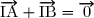
12 - 48
- 48  + 5
+ 5  = 12
= 12 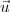 - 43
- 43 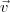
8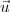 + 3
+ 3 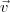 - 5(
- 5(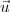 -
- 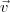 ) = 3
) = 3 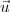 + 8
+ 8 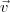
3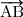 +
+ 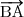 +
+ 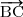 -
- 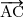 =
= 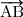
2.
3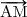 = 3
= 3 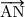 ; M et N sont confondus
; M et N sont confondus
3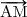 = 2
= 2 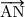 ; A,M,N sont alignés dans cet ordre et AN=1,5 AM.
; A,M,N sont alignés dans cet ordre et AN=1,5 AM.
3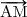 = - 3
= - 3 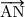 ; A est le milieu de [MN]
; A est le milieu de [MN]
)
)
Publié par Tom_Pascal
le
Vecteurs
exercice 1
1. Construire D tel que2. Construire la parallèle menée par C à (DB).
Cette parallèle rencontre (AB) en G.
3. Calculer
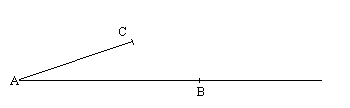
exercice 2
1. Soit I le milieu du segment [AB] et M un point quelconque. Compléter :En déduire
2. Prouver que, s'il existe un point M tel que
3. Compléter :
Conclusion :
I est le milieu de [AB] si et seulement si
exercice 3
1. Simplifier les écritures :12
8
3
2. Que peut-on dire des points M et N dans les cas suivants ?
3
3
3
Dans l'espace :
exercice 4
Les points A et B ont pour coordonnées respectives (2 ; -3 ; 5) et (3 ; 1 ; -2) dans le repère (O,1. Calculer les coordonnées du vecteur
2. Calculer les coordonnées du vecteur
exercice 5
Le point A a pour coordonnées (-4 ; 2 ; -3 ) dans le repère (O,Le vecteur
Quelles sont les coordonnées du point B ?
exercice 2
1. Soit I le milieu du segment [AB] et M un point quelconque. Compléter :Donc
2. D'après la question précédente
Si nous avons un point M tel que
3. Conclusion :
I est le milieu de [AB] si et seulement si
exercice 3
1.12
8
3
2.
3
3
3
exercice 4
exercice 5
B (-2,3,2).
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction