Fiche de mathématiques
Ile mathématiques > maths bac > Bac 2023 toujours : des sujets venus d'ailleurs
Bac Mathématiques
Durée : 3h
Coefficient: 3
Documents autorisés : Néant
8 points
Partie A:
1) Résoudre dans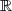 l'équation
l'équation  .
.
2) On donne le polynôme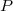 défini pour tout réel
défini pour tout réel  par
par =x^3-13x-12) .
.
a) Calculer) .
.
b) Déterminer trois réels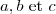 tels
tels =(x+1)(ax^2+bx+c)) .
.
c) En déduire la résolution de l'équation=0) .
.
d) Déduire de la question c) la résolution de l'équation^3-13\ln x-12=0) .
.
3) Résoudre dans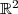 le système:
le système: 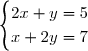 .
.
4) En déduire la solution dans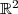 du système:
du système: 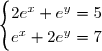 .
.
Partie B:
1-a) Décomposer en produit de facteurs premiers le nombre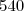 .
.
b) En déduire la valeur du nombre réel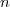 tel que :
tel que : 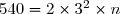 .
.
2) Déterminer deux entiers naturels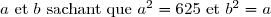 .
.
8 points
Soit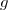 la fonction numérique définie par
la fonction numérique définie par =\dfrac{2x+a}{x+2}) où
où  est un nombre réel.
est un nombre réel.
On désigne par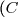) la courbe représentative de
la courbe représentative de 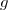 dans un plan muni d'un repère orthonormé
dans un plan muni d'un repère orthonormé ) . Unité graphique
. Unité graphique 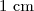 .
.
1) Trouver la valeur de telle que
telle que =-3) .
.
2) Déterminer l'ensemble de définition de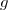 .
.
3) Pour la suite de l'exercice, on prendra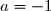 .
.
Calculer les limites aux bornes de l'ensemble de définition de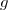 .
.
4) On donne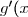=\dfrac{5}{(x+2)^2})
a) Étudier le signe de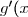) .
.
b) Dresser le tableau de variation de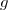 .
.
5) Montrer que la courbe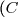) de
de 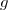 admet le point
admet le point ) comme centre de symétrie.
comme centre de symétrie.
6) Déterminer les asymptotes à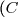) .
.
7) Reproduire et compléter le tableau ci-dessous.
 & &&&&& \\ & &&&&& \\\hline \end{array})
8) Construire la courbe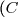) dans le plan.
dans le plan.
4 points
On s'intéresse aux tailles (en cm) des nouveaux nés d'une clinique de la ville en 2019.
Le tableau ci-dessous donne les résultats obtenus.
 }x_i &46&46,5&48&48,5&49&50&53\\\hline \text{ Effecif }n_i && &&&&& \\ \hline \text{ Effectif cumulé croissant} &6&14&24&28&36&38&40 \\\hline \end{array})
1) Reproduire et compléter le tableau ci-dessus.
2) Calculer la taille moyenne des nouveaux nés.
3) A l'aide de cette série statistique, déterminer:
le mode;
la médiane;
le premier et le troisième quartile.
Construire le diagramme en boîte à moustaches de cette série statistique.
Partie A
1) Résolvons l'équation , calculons pour cela le discriminent:
, calculons pour cela le discriminent:
^2-4\times 1\times (-12)=1+48=49>0)
L'équation admet deux solutions réelles:
-\sqrt{49}}{2} = \dfrac{1-7}{2}=-3)
+\sqrt{49}}{2} = \dfrac{1+7}{2}=4)
On obtient:

2-a) Calculons\text{ :})
=(-1)^3-13\times(-1)-12 =-1+13-12=13-13=0\Longrightarrow \boxed{P(-1)=0})
b) Déterminons les trois réels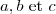 tels que
tels que =(x+1)(ax^2+bx+c)) .
.
=(x+1)(ax^2+bx+c)&\iff& x^3-13x-12=ax^3+bx^2+cx+ax^2+bx+c \\&\iff& x^3-13x-12=ax^3+(a+b)x^2+(b+c)x+c \\&\iff& \begin{cases} a=1\\ 0=a+b\\ -13=b+c\\c=-12\end{cases}\\&\iff& \begin{cases} a=1\\ b=-a=-1\\c=-12\end{cases}\end{matrix})
Vérification:
Donc:
=(x+1)(x^2-x-12)})
c) Déduisons-en les solutions de l'équation=0\text{ :})
=0&\iff& (x+1)(x^2-x-12)=0 \\&\iff& x+1=0\text{ ou }x^2-x-12=0 \\&\iff& x=-1\text{ ou }x=-3\text{ ou }x=4 \end{matrix})
=0\text{ est: }\left\lbrace -3;-1;4\right\rbrace })
d) Résolvons l'équation^3-13\ln x-12=0 \text{ :})
^3-13\ln x-12=0&\iff& \ln x=-3\text{ ou }\ln x=-1\text{ ou }\ln x=4\\&\iff& x=e^{-3}\text{ ou }x=e^{-1}\text{ ou }x=e^4 \end{matrix})

3) Résolvons le système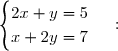
=2\times 5\\x+2y=7\end{cases} \\ &\iff& \begin{cases} 4x+2y=10\\x+2y=7\end{cases} \\ &\iff& \begin{cases} 4x+2y-(x+2y)=10-7\\x+2y=7\end{cases} \\ &\iff& \begin{cases}3x=3\\2y=7-x\end{cases} \\ &\iff& \begin{cases}x=1\\y=\dfrac{7-x}{2}\end{cases} \\ &\iff& \boxed{\begin{cases}x=1\\y=3\end{cases}} \end{matrix} )
Donc:\right\rbrace })
4) Résolvons le système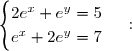

Donc:\right\rbrace })
Partie B
1-a) Décomposons en produit de facteurs premiers le nombre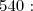
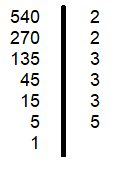
Donc:
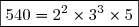
b) Directement:
=2\times 3^2\times 30 )
On en déduit que:
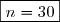
2) Déterminons deux entiers naturels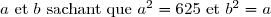 .
.
Décomposons en produit de facteurs premiers le nombre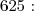
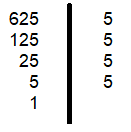
D'où:^2 \text{ , donc: } a=5^2=25) .
.
Et donc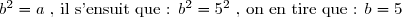
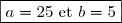
1) On a:
=-3&\iff& \dfrac{-2+a}{-1+2}=-3 \\&\iff& a-2=-3 \\&\iff& \boxed{a=-1} \end{matrix})
2) Notons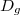 le domaine de définition de la fonction
le domaine de définition de la fonction 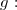
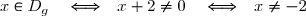
D'où:
![\boxed{D_g=\R\blackslash \lbrace -2\rbrace = ]-\infty;-2[\cup ]-2;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\boxed{D_g=\R\blackslash \lbrace -2\rbrace = ]-\infty;-2[\cup ]-2;+\infty[ })
3) On a:![\forall x\in ]-\infty;-2[\cup ]-2;+\infty[\text{ : }g(x)=\dfrac{2x-1}{x+2}](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]-\infty;-2[\cup ]-2;+\infty[\text{ : }g(x)=\dfrac{2x-1}{x+2})
Calculons les limites aux bornes de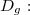
= \displaystyle\lim_{x\to -\infty}\dfrac{2x-1}{x+2}=\displaystyle\lim_{x\to -\infty}\dfrac{2x}{x}=2)
= \displaystyle\lim_{x\to -2^-}\dfrac{2x-1}{x+2}=\dfrac{-4-1}{0^-}=\dfrac{-5}{0^-}=+\infty)
= \displaystyle\lim_{x\to -2^+}\dfrac{2x+5}{x+2}=\dfrac{-4+-1}{0^+}=\dfrac{-5}{0^+}=-\infty)
= \displaystyle\lim_{x\to +\infty}\dfrac{2x+5}{x+2}=\displaystyle\lim_{x\to +\infty}\dfrac{2x}{x}=2)
Récapitulons:
=2 & \displaystyle \lim_{x\to +\infty} g(x)= 2 \\ \displaystyle \lim_{x\to -2^-} g(x)=+\infty & \displaystyle \lim_{x\to -2^+} g(x)=-\infty \end{matrix} })
4-a) On a=\dfrac{5}{(x+2)^2})
Puisque pour tout réel appartenant à
appartenant à ^2>0)
Alors directement:
>0})
[ num]b) Puisque:>0)
Donc:![\text{ La fonction }g\text{ est strictement croissante sur }]-\infty;-2[ \text{ et sur }]-2;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\text{ La fonction }g\text{ est strictement croissante sur }]-\infty;-2[ \text{ et sur }]-2;+\infty[ })
Et on dresse le tableau de variations de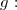
 & & + & &\dbarre & &+ & \\ \hline & & & +\infty &\dbarre & & & 2 \\ g & &\nearrow& &\dbarre & &\nearrow& \\ & 2 & & &\dbarre & -\infty & & \\ \hline \end{array})
Remarque: Il faut mettre double barre en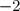 pour indiquer que la fonction
pour indiquer que la fonction 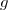 et sa dérivée ne sont pas définies en
et sa dérivée ne sont pas définies en 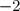 .
.
num]5) Rappelons la définition d'un centre de symétrie:
Soit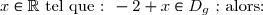
![\begin{matrix}\bullet \enskip -2+x\in D_g&\iff& -2+x\in ]-\infty;-2[\cup ]-2;+\infty[ \\&\iff& -2+x\in ]-\infty;-2[\text{ ou } -2+x\in ]-2;+\infty[ \\&\iff& -2+x<-2 \text{ ou }-2+x>-2 \\&\iff& x<0 \text{ ou }x>0\\&\iff& -x>0 \text{ ou }-x<0\\&\iff& -2-x>-2 \text{ ou }-2-x<-2\\&\iff& -2-x\in ]-2;+\infty[ \text{ ou }-2-x\in ]-\infty;-2[ \\&\iff& -2-x\in ]-\infty;-2[\cup ]-2;+\infty[ \\&\iff& -2-x\in D_g \end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix}\bullet \enskip -2+x\in D_g&\iff& -2+x\in ]-\infty;-2[\cup ]-2;+\infty[ \\&\iff& -2+x\in ]-\infty;-2[\text{ ou } -2+x\in ]-2;+\infty[ \\&\iff& -2+x<-2 \text{ ou }-2+x>-2 \\&\iff& x<0 \text{ ou }x>0\\&\iff& -x>0 \text{ ou }-x<0\\&\iff& -2-x>-2 \text{ ou }-2-x<-2\\&\iff& -2-x\in ]-2;+\infty[ \text{ ou }-2-x\in ]-\infty;-2[ \\&\iff& -2-x\in ]-\infty;-2[\cup ]-2;+\infty[ \\&\iff& -2-x\in D_g \end{matrix})
Et:
+g(-2-x) &=& \dfrac{2(-2+x)-1}{-2+x+2}+\dfrac{2(-2-x)-1}{-2-x+2}\\&=& \dfrac{-4+2x-1}{x}+\dfrac{-4-2x-1}{-2-x+2}\\&=& \dfrac{-5+2x}{x}+\dfrac{-5-2x}{-x}\\&=& \dfrac{-5+2x}{x}+\dfrac{5+2x}{x}\\&=& \dfrac{-5+2x+5+2x}{x}\\&=& \dfrac{4x}{x}\\&=& 4 \\&=& 2\times 2\end{matrix})
Conclusion:
 \text{ de }g \text{ admet le point }I(-2;2) \text{ comme centre de symétrie}})
6) On a=\displaystyle \lim_{x\to +\infty} g(x)= 2) .
.
Donc:
\text{ au voisinage de }-\infty\text{ et de }+\infty \end{matrix}})
De plus:=+\infty \text{ et } \displaystyle \lim_{x\to -2^+} g(x)=-\infty)
\text{ dirigée vers le haut à gauche et vers le bas à droite } \end{matrix}})
7) On calcule les images, on trouve:
 & \dfrac{9}{2}&7&-\dfrac{4}{3}&-\dfrac{1}{2}&0& \dfrac{3}{4}\\ & &&&&& \\\hline \end{array})
8) La figure:
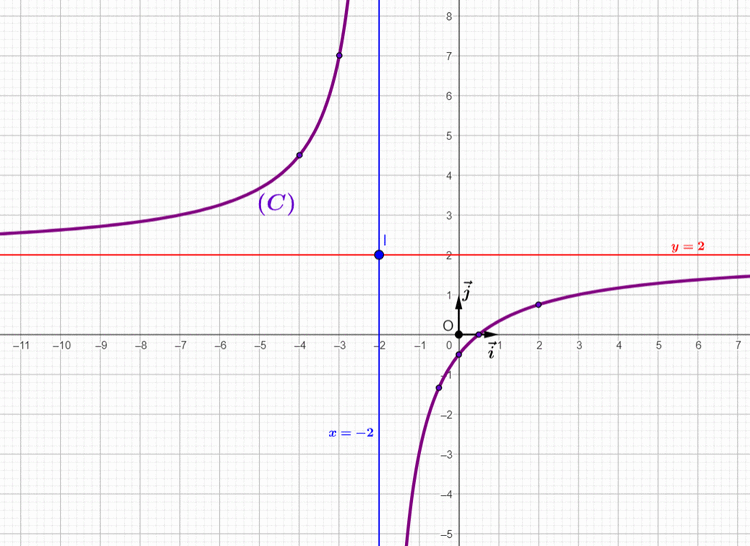
1) Complétons le tableau:
 }x_i &46&46,5&48&48,5&49&50&53\\\hline \text{ Effecif }n_i &6& 14-6=8&24-14=10&28-24=4&36-28=8&38-36=2&40-38=2 \\ \hline \text{ Effectif cumulé croissant} &6&14&24&28&36&38&40 \\\hline \end{array})
2) L'effectif total noté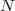 est la somme de tous les effectifs , il correspond au dernier effectif cumulé :
est la somme de tous les effectifs , il correspond au dernier effectif cumulé : 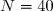
On calcule alors la moyenne de cette série statistique :
 \\&=&\dfrac{1920}{40}\\&=&48\end{matrix})
Donc :
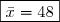
3)
Le mode d'une série statistique est la valeur à laquelle correspond le plus grand effectif.
Ici, le plus grand effectif est 10, donc:

La médiane est la valeur centrale d'une série statistique.
L'effectif total est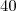 (pair), et
(pair), et 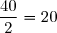
La médiane occupe donc le 20ème rang.
Finalement: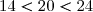 , on en tire que:
, on en tire que:
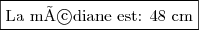
Le premier quartile:
On a: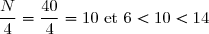
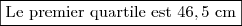
Le troisième quartile:
On a: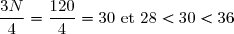
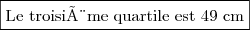
Le diagramme:
Rappelons comment visualiser les données à l'aide d'un diagrammr en boîte à moustaches:
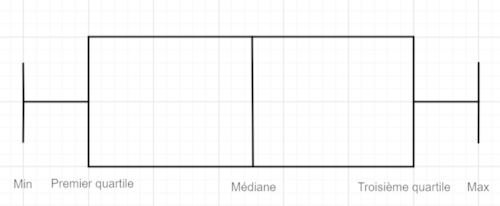
La largeur de la boîte est limitée par le premier et le trosième quartile.
La hauteur de la boîte n'est à priori pas définie, c'est au choix.
Et on trace le diagramme en boîte à moustaches:
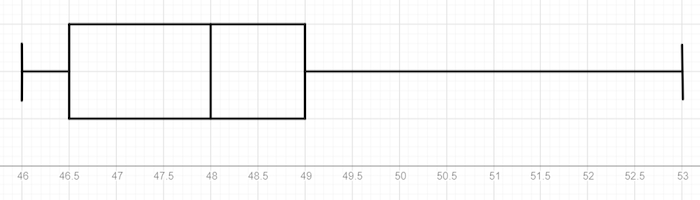
Bac Mathématiques
Congo-Brazzaville 2023
Série A
Coefficient: 3
Documents autorisés : Néant
8 points
exercice 1
Partie A:
1) Résoudre dans
2) On donne le polynôme
a) Calculer
b) Déterminer trois réels
c) En déduire la résolution de l'équation
d) Déduire de la question c) la résolution de l'équation
3) Résoudre dans
4) En déduire la solution dans
Partie B:
1-a) Décomposer en produit de facteurs premiers le nombre
b) En déduire la valeur du nombre réel
2) Déterminer deux entiers naturels
8 points
exercice 2
Soit
On désigne par
1) Trouver la valeur de
2) Déterminer l'ensemble de définition de
3) Pour la suite de l'exercice, on prendra
Calculer les limites aux bornes de l'ensemble de définition de
4) On donne
a) Étudier le signe de
b) Dresser le tableau de variation de
5) Montrer que la courbe
6) Déterminer les asymptotes à
7) Reproduire et compléter le tableau ci-dessous.
8) Construire la courbe
4 points
exercice 3
On s'intéresse aux tailles (en cm) des nouveaux nés d'une clinique de la ville en 2019.
Le tableau ci-dessous donne les résultats obtenus.
1) Reproduire et compléter le tableau ci-dessus.
2) Calculer la taille moyenne des nouveaux nés.
3) A l'aide de cette série statistique, déterminer:
le mode;
la médiane;
le premier et le troisième quartile.
Construire le diagramme en boîte à moustaches de cette série statistique.
exercice 1
Partie A
1) Résolvons l'équation
L'équation admet deux solutions réelles:
On obtient:
2-a) Calculons
b) Déterminons les trois réels
Vérification:
Donc:
c) Déduisons-en les solutions de l'équation
d) Résolvons l'équation
3) Résolvons le système
Donc:
4) Résolvons le système
Donc:
Partie B
1-a) Décomposons en produit de facteurs premiers le nombre
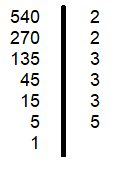
Donc:
b) Directement:
On en déduit que:
2) Déterminons deux entiers naturels
Décomposons en produit de facteurs premiers le nombre
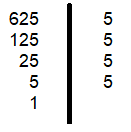
D'où:
Et donc
exercice 2
1) On a:
2) Notons
D'où:
3) On a:
Calculons les limites aux bornes de
Récapitulons:
4-a) On a
Puisque pour tout réel
Alors directement:
[ num]b) Puisque:
Donc:
Et on dresse le tableau de variations de
Remarque: Il faut mettre double barre en
num]5) Rappelons la définition d'un centre de symétrie:
Rappel
Soient 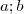 deux réels et soit
deux réels et soit  une fonction définie sur son ensemble de définition
une fonction définie sur son ensemble de définition 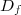 .
.
Un point) est le centre de symétrie de la courbe
est le centre de symétrie de la courbe 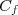 de la fonction
de la fonction  si et seulement si, pour tout réel
si et seulement si, pour tout réel  tel que
tel que 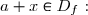
+f(a-x)=2b)
Un point
Soit
Et:
Conclusion:
6) On a
Donc:
De plus:
7) On calcule les images, on trouve:
8) La figure:

exercice 3
1) Complétons le tableau:
2) L'effectif total noté
On calcule alors la moyenne de cette série statistique :
Donc :
3)
Le mode d'une série statistique est la valeur à laquelle correspond le plus grand effectif.
Ici, le plus grand effectif est 10, donc:
La médiane est la valeur centrale d'une série statistique.
L'effectif total est
La médiane occupe donc le 20ème rang.
Finalement:
Le premier quartile:
On a:
Le troisième quartile:
On a:
Le diagramme:
Rappelons comment visualiser les données à l'aide d'un diagrammr en boîte à moustaches:
Rappel

La largeur de la boîte est limitée par le premier et le trosième quartile.
La hauteur de la boîte n'est à priori pas définie, c'est au choix.
Et on trace le diagramme en boîte à moustaches:

ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction forum de terminale
forum de terminale