Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première SuitesTopics traitant de suites [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Calcul approché de Pi par la méthode d'Archimède. Dur..

Posté par Anth0w (invité) 22-02-07 à 00:49

Bonjour,

--
Calcul approché de avec la méthode d'Archimède.

On se propose de déterminer une valeur approché de  en utilisant la méthode d'Archimède.
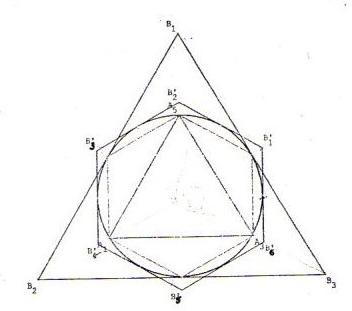
Le périmètre d'un cercle est majoré par celui de tout polygone régulier circonscrit et minoré par tout polygone régulier inscrit. On considère un cercle de rayon 1. Partant d'un triangle équilatéral, on double le nombre de côtés afin d'obtenir un hexagone régulier. On note pn, respectivement qn le demi-périmètre du polygone inscrit; respectivement circonscrit avec n{0;....;2n}. On note Ak les sommets du polygone inscrit et Bk les sommets du polygone circonscrit. Avec les notations du problème on remarque que le polygone possède 3*2n côtés.

I.
1. Quel est la mesure de l'angle AkÔAk+1? et BkÔBk+1?
AkÔAk+1=/3=60°
BkÔBk+1=2/3=120°

2. Calculer p1 et q1. En déduire un premier encadrement de .
Normalement avec Al Kashi: p1=6 et q1=4rac(3) ?
donc 3 2rac(3)

II. Cas général: (c'est là où ça pose véritablement problème)
3. Exprimer AkÔAk+1 en fonction de n. Dans la suite du problème on pose n=/(3*2n) et cn=cosn.
Je trouve donc, AkÔAk+1=2/(3*2n)=360/(3*2n) ..

4. Calculer pn en fonction de n.

5. Montrer que pn=pn+1*cn+1.

6. Exprimer qn en fonction de pn et cn.

--

J'ai un petit problème à partir de la question 4.
Je cherche desesperément, rien à faire! Si quelqu'un pourrait me proposer son aide..
Merci d'avance.

Calcul approché de Pi par la méthode d\'Archimède. Dur..

Posté par
patrice rabillerre : Calcul approché de Pi par la méthode d'Archimède. Dur.. 22-02-07 à 08:20

Bonjour,

Question I.1.

Ton texte n'est pas très sûr : je suppose que tu veux dire k[0,...32n[ (k étant l'indice utilisé pour les sommets et n celui pour les polygones).

Puisque le polygone inscrit n° n possède 32n côtés, alors chacun des angles aux sommets a pour mesure : (2)/(32n).

Autrement dit : 3$\widehat{A_k OA_{k+1}}=\widehat{B_k OB_{k+1}}=\frac{2\pi}{3\times2^n}

Question I.2.

Le périmètre d'un triangle équilatéral inscrit dans un cercle de rayon 1 est égal à 3\sqrt 3. Donc, le demi périmètre est : p_1=\frac{3\sqrt 3}{2}
De même le périmètre du triangle équilatéral circonscrit au cercle de rayon 1 est égal à 6\sqrt 3 donc le demi périmètre est q_2=3\sqrt 3
Ce qui nous donnearait comme premier encadrement de : \frac{3\sqrt 3}{2}\le\pi\le 3\sqrt 3, soit environ 2,5985,196

Posté par Anth0w (invité)re : Calcul approché de Pi par la méthode d'Archimède. Dur.. 22-02-07 à 11:05

Effectivement, l'énoncé n'est pas très clair.. Cependant, le texte dit bien n{0;..,2n} et non k[0,...3*2n[.
Peut-être est-ce une erreur dans l'énoncé ou est-ce que c'est fait exprès ?

Ceci dit, je me suis rendu compte que j'ai mal compris l'exercice.. je vais recommencer ça
Je reviens dans peu de temps, restez à vos claviers!
Merci

Posté par Anth0w (invité)re : Calcul approché de Pi par la méthode d'Archimède. Dur.. 22-02-07 à 11:09

Oui et il y a une erreur en recopiant la question 1.
j'ai oublié de préciser: "pour le cas où n=1 (c'est à dire dans le cas de l'hexagone)"

Posté par
patrice rabillerre : Calcul approché de Pi par la méthode d'Archimède. Dur.. 22-02-07 à 19:37

Alors oui, dans le cas de l'hexagone, les angles ont bien pour mesure /3

Posté par Faquarl (invité)re : Calcul approché de Pi par la méthode d'Archimède. Dur.. 22-02-07 à 19:42

Partirce rabiller : l'expert des approches de pi

Posté par Anth0w (invité)re : Calcul approché de Pi par la méthode d'Archimède. Dur.. 22-02-07 à 21:22

Donc pour le 2., si on utilise le cas de l'hexagone et non pas celui des triangles équilateraux, qu'est-ce que ça donnerait ?

Posté par
patrice rabillerre : Calcul approché de Pi par la méthode d'Archimède. Dur.. 23-02-07 à 06:17

Bonjour,

Je reprends tes questions.

2.) Pour les triangles équilatéraux, il s'agit de n=0.
On obtient comme je l'ai dit : p_0=\frac{3\sqrt 3}{2} (triangle inscrit) et q_0=3\sqrt 3 (triangle circonscrit)

Par contre pour les hexagones (cas n=1) on obtient : p_1=3 et q_1=4\sqrt 3 comme tu l'as toi-même trouvé.

3.) On a bien : \hat{A_kOA_{k+1}}=\frac{2\pi}{3\times 2^n}
Donc, d'après l'énoncé : \hat{A_kOA_{k+1}}=2\theta_n (voir figure ci-dessous.

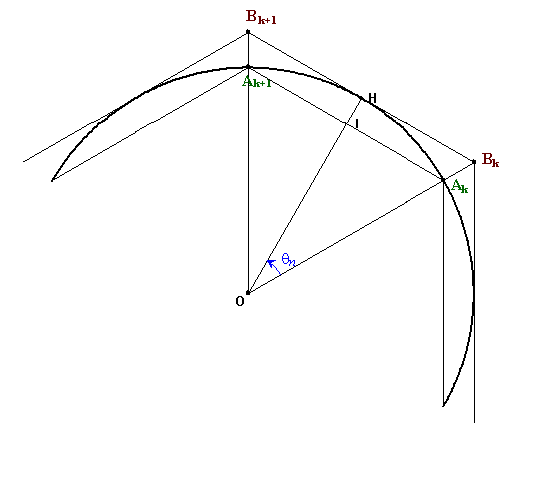
4.) On a : pn=32n IAk (I étant le milieu de [AkAk+1] )
Donc : pn=32n sin n

5.) Donc pn+1=32n+1 sinn+1.
Or n+1=(n)/2

On sait que sin(2a)=2sin a cos a
Donc sin(n)=2 sin(n+1) cos(n+1)

Donc sin(n+1)=(sin(n))/(2cos(n+1))

Donc 4$p_{n+1}=3\times2^{n+1}\frac{\sin \theta _n}{2\cos \theta_{n+1}}

Donc 4$p_{n+1}=\frac{3\times2^{n}\sin \theta _n}{\cos \theta_{n+1}}=\frac{p_n}{{c_{n+1}}

Calcul approché de Pi par la méthode d\'Archimède. Dur..

Posté par toto69 (invité)intérrésant 25-02-07 à 12:31

Je trouve cet exercice intéressant mais cependant pouvais vous m'éclairer pour la question 2, comment trouvez vous q1 ?

Et comme répondre à la question 6, qui me parrait relever ??

Cordialement

Posté par
patrice rabillerre : Calcul approché de Pi par la méthode d'Archimède. Dur.. 25-02-07 à 13:47

Bonjour

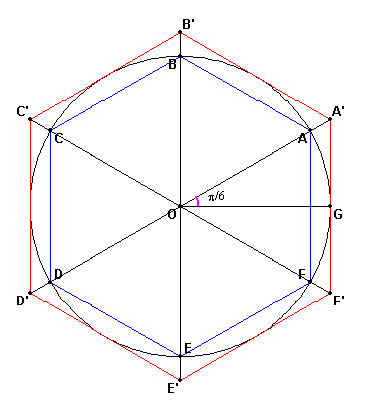
Je me suis trompé Voici le détail du calcul de q1 :

q1 correspond au demi périmètre de l'hexagone circonscrit au cercle de rayon OG = 1 (voir figure ci-dessous)
3$\hat{GOA'}=\pi/6
Donc 3$\frac{GA^'}{OG}=\tan\frac{\pi}{6}=\frac{\sqrt 3}{3}
Donc 3$F^'A^'=2GA^'=\frac{2\sqrt3}{3}
Comme un hexagone possède 6 côtés, le périmètre de l'hexagone A'B'C'D'E'F' est donc égal à 3$\frac{12\sqrt 3}{3}=4\sqrt 3

Donc, sauf nouvelle erreur, q_1=2\sqrt 3

Pour la question 6 :

On peut dire que : 3$\frac{q_n}{p_n}=\frac{GA^'}{IA}=\frac{OG}{OI}=\frac{1}{\cos\theta} (le point I, non noté sur la figure, est le milieu de [AF])
À partir de là, il est facile d'en déduire pn et qn en fonction de n

Calcul approché de Pi par la méthode d\'Archimède. Dur..

Posté par
patrice rabillerre : Calcul approché de Pi par la méthode d'Archimède. Dur.. 25-02-07 à 15:13

Pour être un peu plus complet dans ma dernière réponse ...

On considère les suites :

(n) définie par 0=/3 et n+1=(n)/2

(cn) définie par cn=cos n

(pn) définie par p0=\frac{3\sqrt 3}{3} et pn+1=(pn)/(cn+1)

(qn) définie par qn=(pn)/(cn)

Une fois que l'on sait calculer les termes de la suite (cn), il est très facile de calculer les termes pn et qn.

Montrons le calcul de cn+1 en fonction de cn.

On sait que cos 2a = 2cos²a - 1
On en déduit : cos²a=(cos2a + 1)/2
Par conséquent : 4$\cos^2\theta_{n+1}=\frac{\cos\theta_n+1}{2}
Donc :4$c^2_{n+1}=\frac{c_n+1}{2}
Finalement : 4$c_{n+1}=\sqrt{\frac{c_n+1}{2}}

Un petit programme très simple permet ensuite de calculer les suites (p) et (q) et d'en déduire un encadrement de .

Posté par tut (invité)re : Calcul approché de Pi par la méthode d'Archimède. Dur.. 06-11-07 à 19:00

Bonjours à tous

J'ai exactement le meme problème mais je ne sais pas comment calculer le périmétre du triangle circonscrit au cercle de rayon 1.


Quelqu'un saurait me donner les détails du calcul?

Merci


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !